对于线性时不变电路,如果电路的激励是单一的独立电压源或独立电流源,则网络零状态响应r(t)的象函数R(s)与激励e(t)的象函数E(s)之比为该电路的网络函数H(s),即
![]()
定义网络函数的线性时不变电路(LTI)及其条件可以用图9-14 所示的电路,其中的LTI 网络除输入端1-1′施加激励外,电路的其余部分不含独立电源,且所有储能元件的原始储能均为零。
如图9-14(a)所示,若输入激励E(s)为独立电压源U1(s),则响应可能是I1(s)、I2(s)和U2(s)中的一个;反之,如图9-14(b)所示,若输入激励E(s)是独立电流源I1(s),则响
应可能是U1(s)、I2(s)和U2(s)中的一个。这样,网络函数有6 种类型,分别如下。
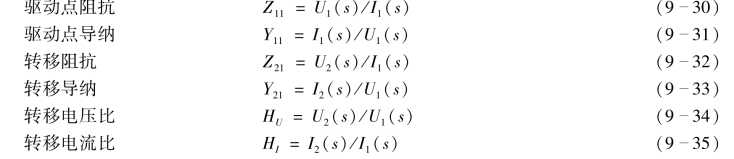
式中,驱动点阻抗和驱动点导纳是指输出响应和输入激励在同一端口的情况,而转移阻抗、转移导纳、转移电压比和转移电流比是指输出响应和输入激励在不同端口的情况。
分析式(9-30)、式(9-31)也会发现,同一端口的驱动点阻抗和驱动点导纳互为倒数关系,即
![]()
但转移阻抗和转移导纳之间不存在这种关系,如式(9-32)、式(9-33)所示。(https://www.daowen.com)
【例9-20】 在图9-15(a)所示电路中,激励是电压源u1(t),求响应分别为uC(t)和iL(t)时的网络函数。
解:由于网络函数H(s)的定义是零状态响应,因此储能元件的初始条件均为零,可画出运算电路如图9-15(b)所示。根据运算电路图可得
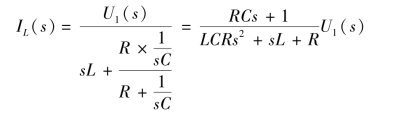
对应网络函数为
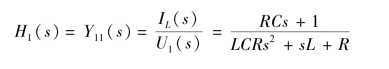
用串联分压可得网络函数,即
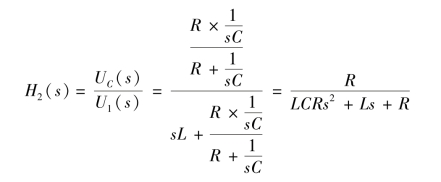
从本例题可以看出,对于同一电路,在同一电源作用下,所选取的输出变量不同,则网络函数不同。由于在线性时不变电路中各元件参数均为常数,所以求出的网络函数一定是实系数有理函数,故网络函数一般形式为
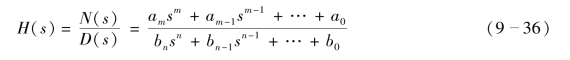
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




