线性动态电路的复频域分析法也称为运算法,它是应用拉氏变换求解线性时不变动态电路时域响应的一种方法。KCL、KVL 和电路元件的VCR 特性方程是施加于电路的两大约束条件,电路分析计算的各种方法都是以这两大约束条件为基本依据推导归纳得到的。通过拉氏变换推导出复频域形式的KCL、KVL 和电路元件的VCR 特性方程,从而把线性时不变动态电路变换成了复频域电路模型。因此,分析计算线性时不变电路的各种方法也适用于复频域电路分析。
电感、电容的运算阻抗和导纳与正弦电流电路的相量法中线性电感、电容的阻抗和导纳的形式相似,仅是以s 替代jω。实际上,运算法和相量法的基本思想类似,相量法把正弦量用相量表示,其目的是简化正弦函数计算,运算法把时间函数变换为对应的象函数,将时域中线性微分方程转换为复频域中线性代数方程。当电路的所有独立初始条件为零时,对于同一电路列出的相量方程和零状态下的运算形式的方程在形式上相似,但这两种方程具有不同的意义。在非零初始状态下,电路方程的运算形式中还应考虑附加电源的作用。
复频域分析法的主要步骤如下。
(1)根据时域电路模型图,计算换路前电路中的电感电流iL(0-)和电容电压uC(0-),确定运算电路中电感和电容的附加电源,画出换路后的运算电路。
(2)根据具体电路选用合适的电路分析方法,列写出运算形式的电路方程,并求出待求量的象函数。
(3)应用部分分式展开法对待求量的象函数进行拉氏反变换,求得待求量的原函数。
【例9-15】 如图9-9(a)所示为RC 串联电路,激励为电压源uS(t),电容电压初始状态uC(0-)=0。
(1)若uS(t)=ε(t)V,试求电路响应uC(t);
(2)uS(t)=δ(t);试求电路响应uC(t)。
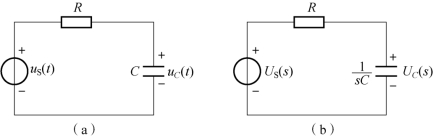
图9-9 例9-15 图
(a)时域电路;(b)s 域运算电路
解:s 域运算电路如图9-9(b)所示。
(1)当uS(t)=ε(t)时,![]() ,故
,故
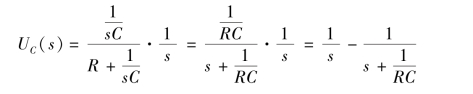
其拉氏反变换为
![]()
(2)当uS(t)=δ(t)时,US(s)=1,故
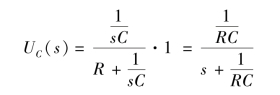
其拉氏反变换为
![]()
以上结果分别为RC 串联电路的阶跃响应和冲激响应。
【例9-16】 电路如图9-10(a)所示,开关S 断开前电路已处于稳态。设t=0 时开关S 断开,试求全响应iL、uL和uC。
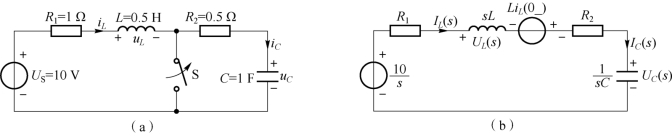
图9-10 例9-16 图
(a)时域电路;(b)s 域运算电路
解:开关断开前的电感电流iL(0-)和电容电压uC(0-)为
![]()
将时域电路图转换为复频域(s 域)电路图如图9-10(b)所示。注意电感附加电源的极性。
根据图9-10(b)可列出电路方程,即(https://www.daowen.com)
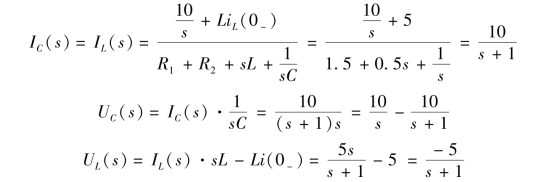
进行拉氏反变换分别得到时域响应,即
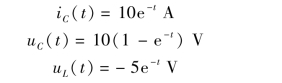
【例9-17】 电路如图9-11(a)所示,已知iL1(0-)=iL2(0-)=0,t=0 时开关S 闭合,求iL1和iL2。
解:储能元件的初始状态为零,做出换路后的运算电路如图9-11(b)所示。以两个电感电流方向为回路绕行方向,列写回路电流方程,即
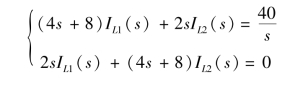
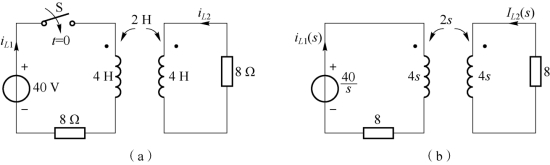
图9-11 例9-17 图
(a)时域电路;(b)s 域运算电路
联立解方程组得
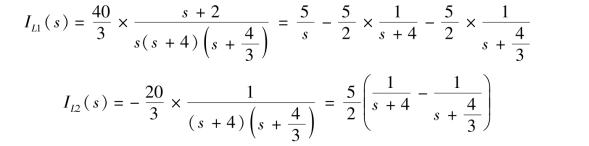
通过拉氏反变换求得时域响应为
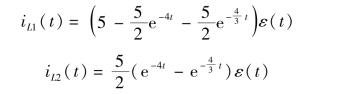
【例9-18】 图9-12(a)所示电路已处于稳态,当t=0 时开关S 闭合,求响应i。
解:换路前,![]() ,uC(0-)=2× iL(0-)=(2×5)V=10 V
,uC(0-)=2× iL(0-)=(2×5)V=10 V
做出换路后的运算电路如图9-12(b)所示。列写结点方程为

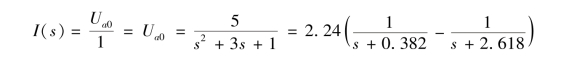
进行拉氏反变换,换路后i(t)由固定值10 A 加暂态响应组成,所以
![]()
【例9-19】 电路如图9-13 所示,已知iL(0-)=0 A,t=0 时将开关S 闭合,求t>0 时的uL(t)。
解:时域电路如图9-13(a)所示,运算电路如图9-13(b)所示。
设参考结点如图9-13(b)所示,取U1(s)为结点电压,对结点a 可列出方程为
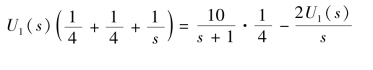
整理可得
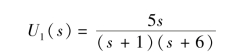
故有
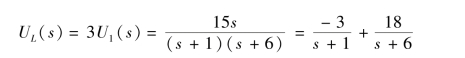
通过拉氏反变换得到
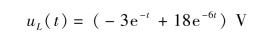
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






