根据元件电压、电流的时域关系，可以推导出各元件电压电流关系的运算形式。

1.电阻

电阻的电路模型如图9-2 所示。

图9-2（a）为电阻元件的时域电路，电阻元件的电压和电流关系为

两边取拉氏变换，得

图9-2　电阻的电路模型

（a）时域电路；（b）s 域运算电路

式（9-22）就是电阻VCR的运算形式，从而可得到图9-2（b）所示的电阻R的s 域运算电路。

2.电感

电感的电路模型如图9-3 所示。

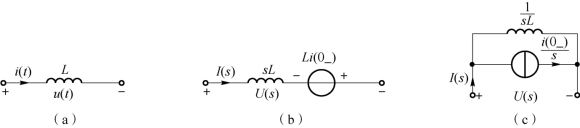
图9-3　电感的电路模型

（a）时域电路；（b）s 域电压源型运算电路；（c）s 域电流源型运算电路

图9-3（a）为电感的时域电路，电感在时域中电压和电流的关系有

两边取拉氏变化，并根据拉氏变换的微分性质得

式（9-23）中sL 为电感的运算阻抗，与正弦电流电路的相量法中线性电感的阻抗形式相似，仅是以s 替代jω 而已。i（0－）表示电感中的初始电流。由式（9-23）可以得到图9-3（b）所示的s 域电压源型运算电路，该电路不仅有电感元件，还有一个附加电压源，Li（0－）表示附加电源的电压，它反映了电感中初始电流的作用，但它的参考极性与i（0－）的参考方向为非关联参考方向。

将式（9-23）变换一下可得

由式（9-24）就可以得到图9-3（c）所示的s 域电流源型运算电路，该电路中为电感的运算导纳，与相量法中线性电感的导纳也相似，仅是以s 替代jω 而已，以表示附加电流源的电流，但它的参考方向与i（0－）的参考方向一致。

3.电容

电容的电路模型如图9-4 所示。

图9-4（a）为电容的时域电路，电容在时域中电压和电流的关系有

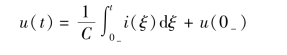
图9-4　电容的电路模型

（a）时域电路；（b）s 域电压源型运算电路；（c）s 域电流源型运算电路

取拉氏变换并根据拉氏变换的积分性质得

也可以变换为

根据式（9-25）、式（9-26）可以分别得到图9-4（b）、（c）所示电容的s 域电流源型运算电路，不仅包括运算阻抗或运算导纳sC，还包括附加电源或Cu（0－）。附加电源反映了电容初始电压的作用，与电感一样，电容的运算阻抗和导纳与正弦电流电路的相量法中线性电容的阻抗和导纳的形式相似，仅是以s 替代jω 而已，图9-4（b）附加电源的极性与u（0－）的参考极性相同，图9-4（c）电流源的极性与u（0－）的参考极性为非关联参考方向。图9-3（c）、图9-4（c）的电流源型运算电路可通过电源相互等效的方法得到。

式（9-22）、式（9-23）、式（9-24）、式（9-25）和式（9-26）分别是线性电阻、线性电感和线性电容的伏安特性的运算形式，根据R、L、C 元件伏安特性可以推导出RLC串联电路伏安特性的运算形式。

4.RLC 串联电路(www.daowen.com)

RLC 串联电路如图9-5 所示。

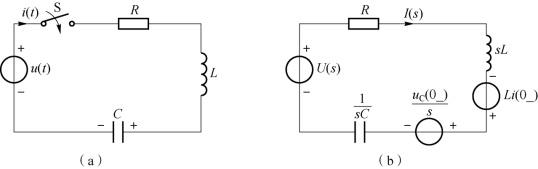
图9-5　RLC 串联电路

（a）时域电路；（b）s 域运算电路

RLC 串联电路时域电路如图9-5（a）所示，设电源电压为u（t），电感中初始电流为i（0－），电容中初始电压为uC（0－），t＝0 时换路，换路后，其s 域运算模型如图9-5（b）所示。根据∑U（s）＝0，有

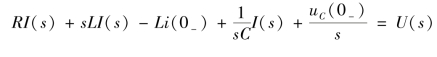
整理得

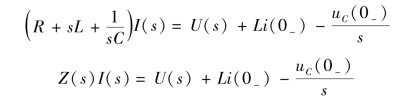
式中，称为RLC 串联电路的运算阻抗。在零初始条件下，i（0－）＝0，uC（0－）＝0，则有

式（9-27）称为欧姆定律的运算形式。

5.耦合电感元件

耦合电感电路如图9-6 所示。

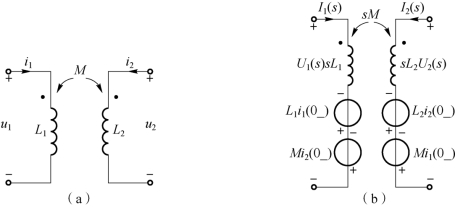
图9-6　耦合电感电路

（a）时域电路；（b）s 域运算电路

耦合电感电路的时域电路如图9-6（a）所示，在图示参考方向下的时域伏安特性方程为

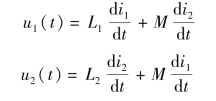
对上式两边取拉氏变换有

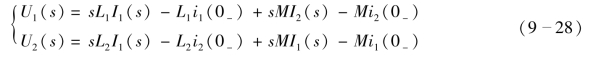
式中，sM 称为互感运算阻抗，Mi1（0－）和Mi2（0－）都是附加电压源，附加电压源的方向与电流i1、i2的参考方向有关。式（9-28）是耦合电感在s 域的伏安特性，由该伏安特性可以得到图9-6（b）所示的s 域运算电路。

6.受控源

如果受控源（线性）的控制电压或电流是运算量，则受控源的电压或电流也是相应线性受控关系的运算量。现以图9-7（a）的时域为例，此时有

运算形式为

图9-7（b）为s 域运算电路。

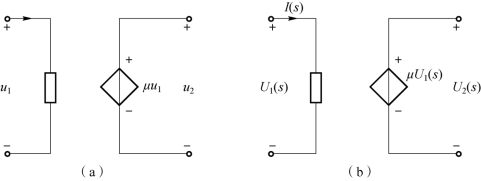
图9-7　受控源的运算模型

（a）时域电路；（b）s 域运算电路

【例9-14】　电路如图9-8 所示，当t＝0 时开关打开，画出运算电路。

解：先计算求得开关打开前电容电压和电感电流的初始值，根据图9-8（a）可求得

根据电容和电感的运算电路可以得到如图9-8（b）所示的s 域运算电路。

图9-8　例9-14 电路

（a）时域电路；（b）s 域运算电路