当高阶线性电路求解时域响应时,常常应用拉氏变换分析问题,在应用中首先要将时域中的参量变换为复频域中的参量,然后求得用象函数表示的解,最后,还需要将所求结果的象函数进行拉氏反变换,以求得时域中的解。
拉普拉斯反变换的定义式为
![]()
计算这一积分要用到复变函数的积分,计算较为烦琐,因而在工程上一般不用此公式。实际上,对于线性集总参数电路,其元件值是常数,因此,其未知电压和电流的s 域表达式也是s的有理函数,如果能求出s的有理函数的反变换,就可以求出电流和电压的时域表达式,以下将介绍一种简单而又系统的求有理函数反变换的方法——部分分式展开法,用部分分式展开法处理,变为表9-1 所列的形式,根据对应关系求拉氏反变换。
电路响应的象函数通常可以表示为一个s的有理分式,即
![]()
式中m 和n 为正整数,且n≥m。
用部分分式展开有理分式F(s)时,需要将有理分式化为真分式,若n >m,则F(s)为真分式,若n=m,则F(s)可写为
![]()
式中,A 是常数,其对应的时间函数为Aδ(t),余数项![]() 是真分式。
是真分式。
用部分分式展开真分式时,要对分母多项式D(s)作因式分解,求出D(s)=0的根,D(s)=0的根可能是单根、共轭复根和重根,以下分别介绍这3 种情况的部分分式反变换。
1.单根
如果D(s)=0 有n 个单根,设这n 个单根分别是p1,p2,…,pn,那么F(s)可以展开为
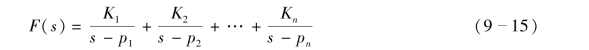
式中K1,K2,…,Kn是待定系数。
将式(9-15)两边都乘以(s-p1),得
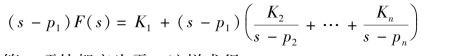
令s=p1,则等式除第一项外都变为零,这样求得
![]()
同理可求得其他系数。所以确定式(9-13)中各待定系数的公式为
![]()
因为pi是D(s)=0的一个根,故关于Ki的式(9-16)为![]() 型不定式,可以用求极限的方法确定Ki的值,即
型不定式,可以用求极限的方法确定Ki的值,即
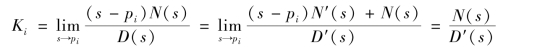
所以确定式(9-16)中各待定系数的另一公式为
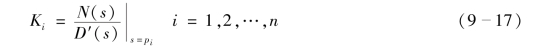
确定了式(9-15)中各待定系数后,相应的原函数为
![]()
【例9-10】 求![]() 的原函数f(t)。
的原函数f(t)。
解:由D(s)=s3+5s2+6s=s(s+2)(s+3)=0,可求出D(s)=0的根为
![]()
则F(s)可分解为
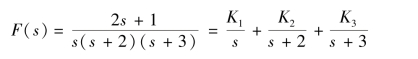
方法一:
根据式(9-16)有
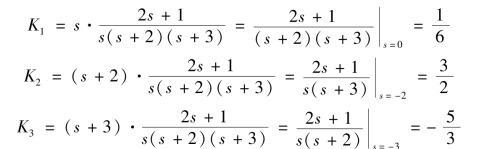
方法二:
根据式(9-17)有
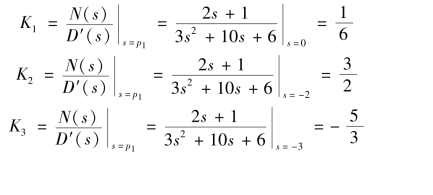
故原函数为
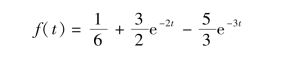
2.共轭复根
如果D(s)=0 具有共轭复根p1=α+jω,p2=α-jω,则
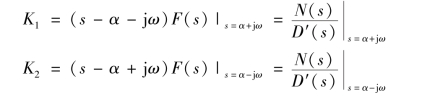
由于F(s)是实系数多项式之比,所以K1、K2为共轭复数。
设K1=|K1|ejθ1,则K2=|K1|e-jθ1,有
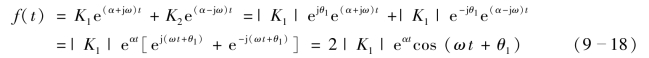
式(9-18)的结果应用到了欧拉公式![]() 。
。
【例9-11】 求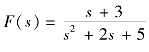 的原函数f(t)。
的原函数f(t)。
解:方法一:
D(s)=s2+2s+5=0的根为共轭复根,分别为p1=-1+j2,p2=-1-j2。
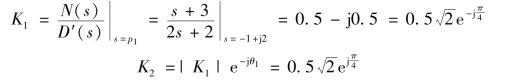
根据式(9-18)可得
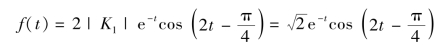 (www.daowen.com)
(www.daowen.com)
方法二:
此象函数可以分解为
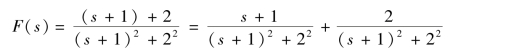
根据表9-1 中三角函数与象函数的对应关系以及复频域平移特性式(9-9)可得
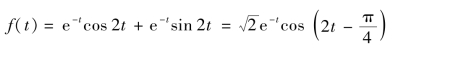
3.重根
如果D(s)=0 具有n 重根,则应含(s-p1)n的因式。先假设D(s)中含有(s-p1)3的因式,p1为D(s)=0的三重根,其余为单根,F(s)可分解为
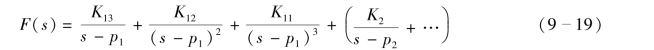
对于单根的系数确定仍采用式(9-17)计算。
将式(9-19)两边都乘以(s-p1)3,则K11被单独分离出来,即
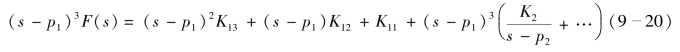
则
![]()
再对式(9-20)两边对s 求导一次,K12被分离出来,即
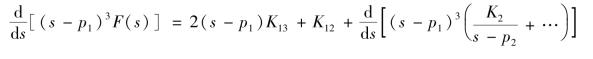
所以
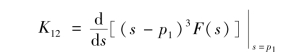
用同样方法可求得
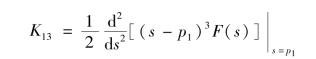
从以上分析过程可以推广到当D(s)=0 具有q 阶重根,其余为单根的分解式为
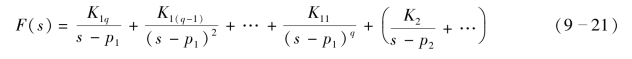
式中
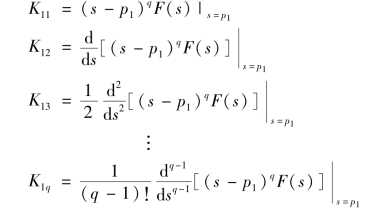
如果D(s)=0 具有多个重根时,对每个重根分别应用上述方法即可得到相应系数。
【例9-12】 求![]() 的原函数f(t)。
的原函数f(t)。
解:D(s)=s3(s+3)2=0的特征根p1=0 为三重根,p2=-3 为二重根。F(s)可分解为
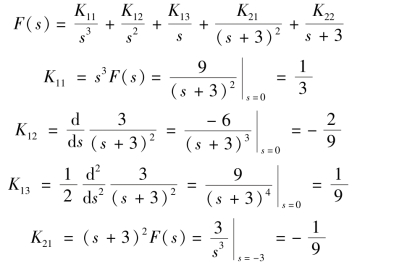
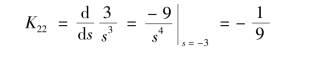
所以
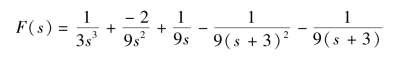
相应的原函数为
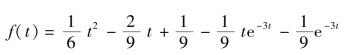
【例9-13】 用拉氏变换法解下述微分方程。
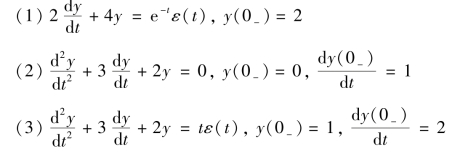
解:(1)对微分方程两边取拉氏变换,得
![]()
代入初始条件并整理得
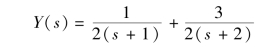
进行拉氏反变换得
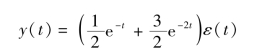
(2)对微分方程两边取拉氏变换,得
![]()
代入初始条件并整理得
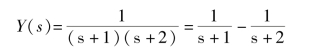
进行拉氏反变换得
![]()
(3)对微分方程两边取拉氏变换,得
![]()
代入初始条件并整理得
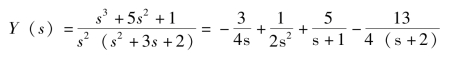
进行拉氏反变换得
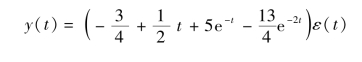
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







