拉普拉斯变换的基本性质简介

学习和掌握拉氏变换的一些常用的基本性质，有助于求解一些较复杂的原函数的象函数，也方便拉氏变换在电路分析中的应用。

1.线性性质

如果L（f（t）]＝F（s），则对于任意常数k，有

如果L[f1（t）]＝F1（s）、L[f2（t）]＝F2（s），则对于任意常数k1和k2，有

证明：

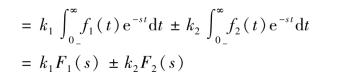
由式（9-2）和式（9-3）可知拉氏变换满足齐次性和可加性，是线性变换。

【例9-4】　余弦函数cos（ωt）和K（1－e－at）的定义域为[0，∞），求其象函数。

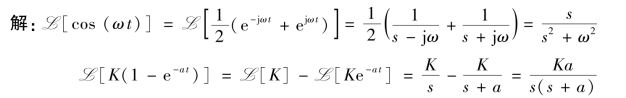
由此可见，根据线性性质，可以将较复杂的函数分解为典型的简单函数，先求各简单函数的象函数，然后再进行组合。

2.微分性质

如果，则

式（9-4）中，f（0－）为原函数f（t）在t＝0－时的值。

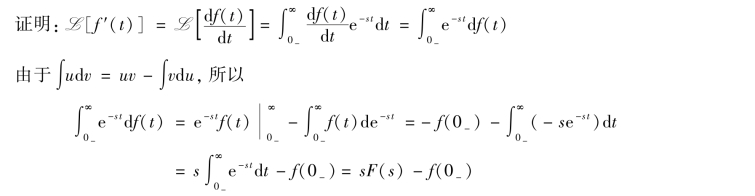
当F（s）存在时，只要Re（s）＝σ 足够大，当t→∞时，e－stf（t）→0，由此类推，得

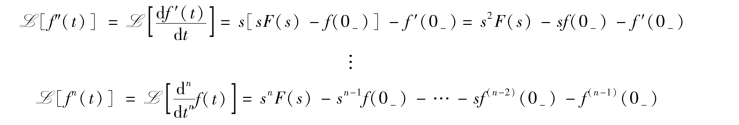
【例9-5】　求冲激函数f（t）＝δ（t）的象函数。

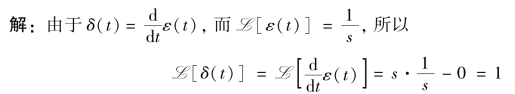
此结果与【例9-3】 用定义法求得的结果完全相同。

3.积分性质

如果L[f（t）]＝F（s），则

证明：因为，两边进行拉氏变换，并由式（9-4）微分性质可得

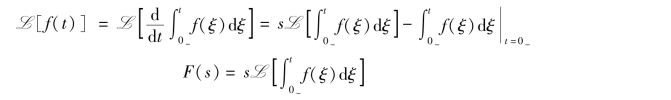
故

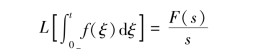
式（9-5）说明，原函数f（t）从0－到t的积分的象函数等于它的象函数F（s）除以s。

【例9-6】　利用积分性质求函数f（t）＝t 和f（t）＝sin（ωt）的象函数。

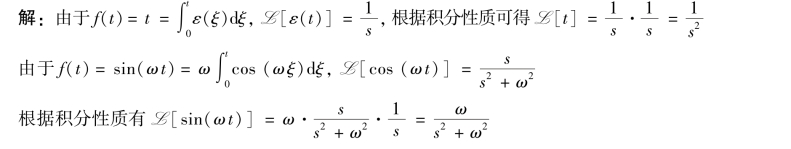
4.初值定理和终值定理

初值定理：如果L[f（t）]＝F（s），则

证明：首先，一阶导数的算子变换为

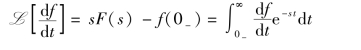
取s→∞时的极限，即

当s→∞时，（df/dt）e－st→0，因此上式最右端第二个积分式的极限为零，于是有

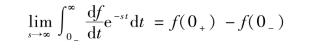
因为f（0－）与s 无关，有

所以

初值定理证明完毕。

终值定理：如果L[f（t）]＝F（s），则

证明：终值定理的证明与初值定理的证明相似，只是取s→0 时的极限，有

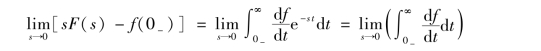
因为上式最右项中积分上限为无穷大，该积分也可以写为极限形式，即

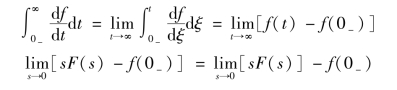
所以

终值定理证明完毕。(https://www.daowen.com)

【例9-7】　已知某象函数为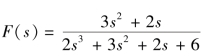，求原函数的初值和终值。

解：根据拉氏变换初值定理和终值定理，有

所以

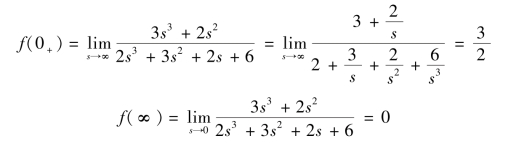
5.时域平移性质

如果L[f（t）ε（t）]＝F（s），则

证明：

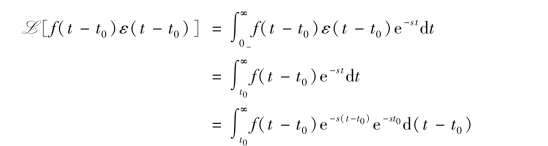
令τ＝t－t0，则上式可变换为

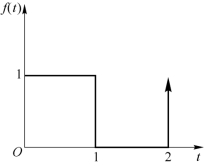
图9-1　例9-8 图

对于一些矩形脉冲波和任意阶梯波，由于它们可用单位阶跃函数和延迟单位阶跃函数来表示，因此利用时域平移性质可直接写出这些波形的象函数。

【例9-8】　求图9-1 所示波形的象函数。

解：图9-1 中波形的时域解析式为

因为，根据时域平移性质，所以

6.复频域平移性质

如果L[f（t）]＝F（s），则

在时域中乘以负指数，相当于延迟，对应于频域中平移。

该性质在进行拉氏反变换时应用较多。

【例9-9】　求下列函数的象函数。

(1)3e－2tcos(2t)　(2)e－2tε(t－1)

解：（1）因为，根据频域平移性质，所以

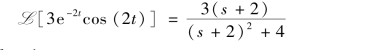
（2）根据时域平移性质，有

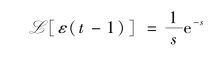
再根据频域平移性质，有

7.卷积定理

设有两个时域函数f1（t）和f2（t），它们在t<0 时为零，f1（t）和f2（t）的卷积定义为

拉氏变换的卷积定理：如果L[f1（t）]＝F1（s），L[f2（t）]＝F2（s），则

证明：根据拉氏变换定义，有

根据延迟的单位阶跃函数的定义，即

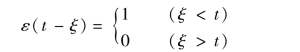
得

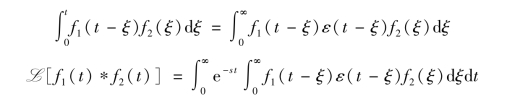
令x＝t－ξ，则e－st＝e－s（x＋ξ），上式变为

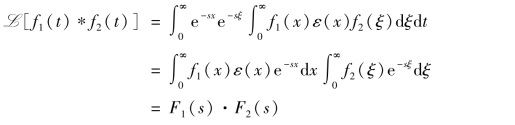
同理，可以证明

所以

根据拉氏变换的定义及与电路分析有关的拉氏变换的一些基本性质，可以方便地求得一些常用的时间函数的象函数，如表9-1 所示。

表9-1　常用的时间函数和象函数

续表