MATLAB 在控制系统的分析、仿真与设计方面应用非常广泛。MATLAB 语言在工程计算方面具有无可比拟的优越性，它集计算、数据可视化和程序设计于一体，其特点有如下。

（1）功能强大。有强大的运算功能，功能丰富的工具箱和强大的文字处理功能。

（2）人机界面友好，编程效率高。

（3）有智能化的作图功能。

（4）具有Simulink 动态仿真功能。

动态电路时域分析的基本方法是建立微分方程并求解，得到电压或电路的响应表达式，最后根据响应表达式手工准确画出响应曲线。

【例8-19】　通过MATLAB 求解一阶RC 电路零输入响应，并显示输出结果。

解：RC 零输入响应电路图如图8-53 所示。

根据KVL 得到微分方程，即

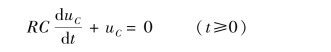
编写MATLAB 程序求解该微分方程的解，并画出电压响应曲线，程序代码如下。

图8-54 为程序运行结果，它直观展示了电容电压与电路时间常数之间的关系。

电路时间常数RC的大小决定着电容电压放电的快慢，改变RC的值，可以方便地绘出响应曲线

【例8-20】　通过MATLAB 求解RLC 串联二阶动态电路，并画出波形图。

解：RLC 串联动态电路如图8-55 所示。

根据KVL 及电感电容的伏安特性，可列出二阶微分方程，即(www.daowen.com)

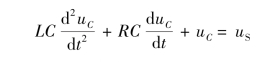
编写MATLAB 程序求解该微分方程的解，并绘制波形图过程如下。

MATLAB 中给出了若干求解一阶微分方程组的函数，如ode23、ode45 等，其调用格式为

使用ode45 函数解此微分方程，要把该二阶微分方程改写为一阶微分方程组，即

然后，在MATLAB 中创建一个M 文件myfun（），代码如下。

二阶线性非齐次方程的特征方程为

解特征方程求得特征根为

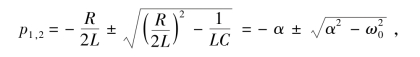
式中，α 被称为衰减系数，改变α的值，就可以得到不同的响应曲线，程序运行结果如图8-56 所示。随着α的减小，电容电压和电流的响应由阻尼非震荡到衰减振荡再到等幅振荡。

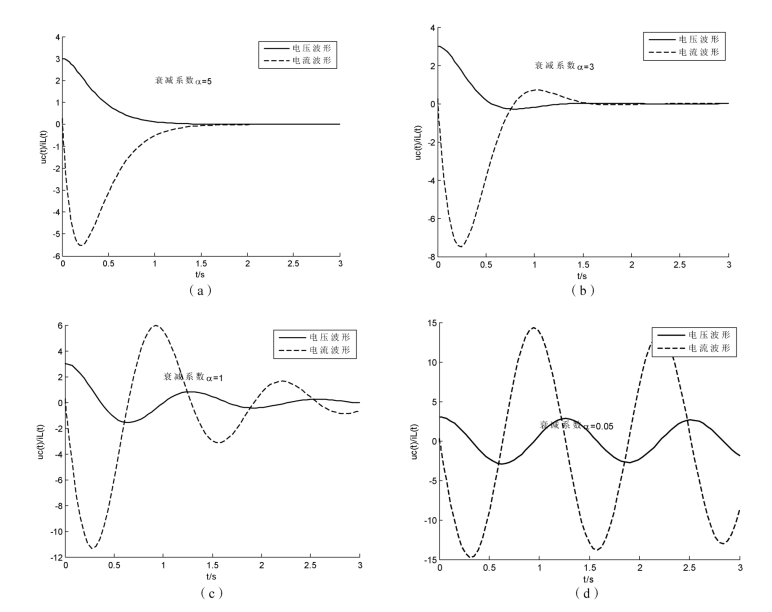
图8-56　程序运行结果——不同衰减系数的电容电压、电流响应曲线

（a）α＝5；（b）α＝3；（c）α＝1；（d）α＝0.05