当输入激励是任意函数时，在时域中可通过卷积积分来求电路的零状态响应。

卷积积分的基本思想：将电路激励函数的波形分解为一系列冲激函数的叠加，对于线性时不变电路，电路的响应等于一系列冲激响应的叠加。

设输入激励f（t）的波形如图8-50 所示。

作用于电路的时间为t0~t，将区间[t0，t]分为n 等分，每等分的宽度为Δt，显然，Δt＝t1－t0＝t2－t1＝…＝t－tn－1。于是，f（t）可用图示的阶梯曲线来逼近，或可以看作是宽度为Δt的一系列矩形脉冲fΔt（t）的叠加，这一系列矩形脉冲可以通过单位脉冲函数和延迟的单位脉冲函数，即pΔt（t）和pΔt（t－tk）来表示。这样输入激励fΔt（t）就可以用上述矩形脉冲表示为

显然，当n →∞时，pΔt（t－tk）→δ（t－tk），故f（t）可以用一系列的冲激函数的叠加来表示。

设线性时不变电路在单位脉冲函数pΔt（t）激励下的零状态响应为hΔt（t），对每一延迟的矩形脉冲pΔt（t－tk），因此电路在f（t）激励下的零状态响应为

当n →∞时，离散变量tk变为连续变量τ，Δt →dτ，hΔt（t－tk）→h（t－τ），求和变为积分，fΔt（t）→f（t），rΔt（t）→r（t）。于是，电路对于任意输入激励f（t）的零状态响应为

若t0＝0 ，则

利用换元积分可得

式（8-46）、式（8-47）和式（8-48）均称为卷积积分。

对于线性时不变电路，求给定任意激励函数f（t）的零状态响应，可以通过计算相应的冲激函数h（t）与输入激励函数f（t）的卷积积分来求得。

【例8-17】　如图8-51 所示RC 串联电路，其中R＝500 kΩ，C＝1 μF，电压源电压为uS＝4e－tε（t）V，设电容上初始电压为零，试求uC（t）。(www.daowen.com)

解：令uS＝δ（t），容易解得电路的冲激响应为

应用卷积积分式（8-48）可得

【例8-18】　设例8-18 中的uS为图8-52 所示的矩形脉冲，试求uC（t）。

解：uS（t）波形为如图8-52 所示，其解析式为

应用卷积积分式（8-47）得电路的零状态响应uC（t）为

式中

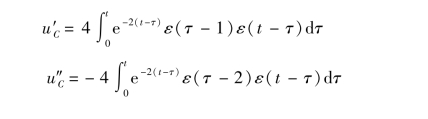
式中，ε（τ－1）ε（t－τ）构成闸门函数，其开放区间为1< τ< t，积分结果对t > 1 成立，因此

同理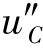，中ε（τ－2）ε（t－τ）也构成闸门函数，其开放区间为2< τ< t，积分结果对t > 2成立，因此

故电路的零状态响应为