【摘要】:二阶电路储能元件的初始储能为零,即电容电压和电感电流都为零,仅由外部激励引起的响应称为二阶电路的零状态响应。二阶电路的零状态响应如图8-48 所示。解:开关S 打开后电路的微分方程为特征方程为代入数据为解得特征根为由于特征根是重根,因此电路为临界阻尼情况,其解为有初始值确定常数K1和K2,即解得所以求得零状态响应为
二阶电路储能元件的初始储能为零,即电容电压和电感电流都为零,仅由外部激励引起的响应称为二阶电路的零状态响应。
二阶电路的零状态响应如图8-48 所示。
图8-48 中为RLC 并联电路,储能元件的初始状态为
![]()
当t=0 时,开关S 打开。根据KCL 有
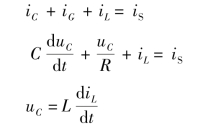

式(8-44)为二阶线性非齐次微分方程,它的解由特解和对应齐次方程的通解组成,即
![]()
式中,特解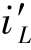 为稳态解,通解
为稳态解,通解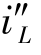 与零输入响应形式相同,再根据初始条件确定积分常数。
与零输入响应形式相同,再根据初始条件确定积分常数。
微分方程式(8-44)的特征根为
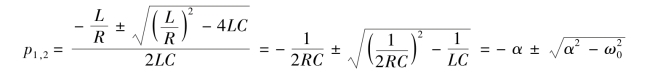
与RLC 串联电路相似,RLC 并联电路的自由分量(通解)同样存在过阻尼、临界阻尼、欠阻尼三种情况,方程的稳态解(特解)i′=iS。
三种情况下的iL分别为
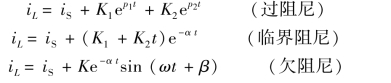
式中,![]() ,常数K1、K2、K、β 由
,常数K1、K2、K、β 由![]() 确定,且
确定,且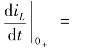
![]() 。(www.daowen.com)
。(www.daowen.com)
【例8-15】 电路如图8-48 所示,R=500 Ω,C=1 μF,L=1 H,iS=1 A,当t=0时,开关S 打开。试求t ≥0 时的iL、uC和iC。
解:开关S 打开后电路的微分方程为
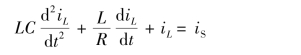
特征方程为
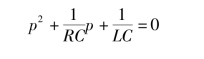
代入数据为
![]()
解得特征根为
![]()
由于特征根是重根,因此电路为临界阻尼情况,其解为
![]()
有初始值确定常数K1和K2,即
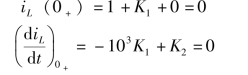
解得
![]()
所以求得零状态响应为
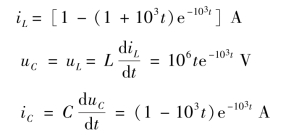
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关电路理论及应用的文章







