用二阶微分方程描述的动态电路称为二阶电路,它包含两个独立的动态元件。在二阶电路中,由储能元件的初始值决定的响应称为二阶电路的零输入响应。二阶电路的初始条件应有两个,RLC 串联二阶电路的零输入响应内容如下。
RLC 串联电路如图8-41 所示,假设电容原已充电,其电压为U0,因为当t< 0 时开关打开,电感中的初始电流为0。当t=0 时,开关S 闭合,此电路的放电过程就是二阶电路的零输入响应。
在指定的电压、电流参考方向下,根据KVL 可得
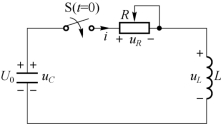
图8-41 RLC 串联电路
![]()
以uC为变量列写微分方程,即
![]()
将以上式代入电压方程,得

式(8-38)是以uC为未知量的RLC 串联电路放电过程的微分方程。这是一个线性常系数二阶齐次微分方程。解这类方程仍然设uC=Aept,然后再确定其中的p 和A。
将uC=Aept代入式(8-38),得特征方程为
![]()
解特征方程求得特征根为
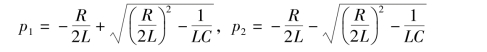
根的性质不同,响应的变化规律也不同。
当R![]() 时,p1、p2为两个不等负实根,则
时,p1、p2为两个不等负实根,则
![]()
当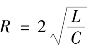 时,p1、p2为两个相等负实根,则
时,p1、p2为两个相等负实根,则
![]()
当 时,p1、p2为一对共轭复根,p1,2=-δ ± jω,则
时,p1、p2为一对共轭复根,p1,2=-δ ± jω,则
![]()
可见特征根仅与电路参数和结构有关,与激励和初始储能无关。
1.过阻尼条件——非振荡放电过程
 为过阻尼条件,即非振荡放电过程,其特征根p1、p2是不等负实根,电压uC可写为
为过阻尼条件,即非振荡放电过程,其特征根p1、p2是不等负实根,电压uC可写为
![]()
确定初始条件,即
![]()
由于
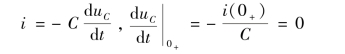
根据初始条件和式(8-39),得

解式(8-40),得
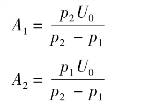
将解得的A1、A2代入式(8-39)就可以得到RLC 串联电路零输入响应的表达式。电容上的电压为

电流为

由于![]() ,故电流也可以写为
,故电流也可以写为

电感电压为

由此可见,uC(t)和i(t)均为随着时间衰减的指数函数,电路的响应为非振荡响应,响应曲线如图8-42所示。
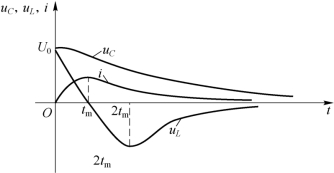
图842 非振荡放电过程中uC、i、uL
图8-42 画出了uC(t)、uL(t)和i(t)随时间变化的曲线。由图可知,uC、i 始终不改变方向,而且有uC≥0 ,i ≥0 ,表明电容在整个过程中一直释放储存的电能,因此称为非振荡放电,又称为过阻尼放电。
当t=0+时,i(0+)=0 ,当t →∞时放电过程结束,i(∞)=0 ,所以在放电过程中电流必然要经历从小到大再趋于零的变化。电流到达最大值的时刻tm可由![]() 求得,即
求得,即

当t< tm时,电感吸收能量,磁场增强;
当t > tm时,i 减小,uL<0,电感释放能量,磁场逐渐衰减,趋向消失;
当t=tm时,电感电压为零。
当t=2tm时,uL极小;
当t > 2tm时,uL衰减加快,能量转换关系如图8-43 所示。
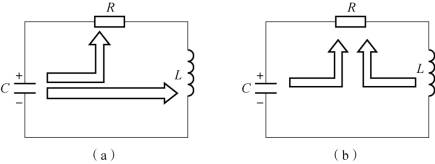
图8-43 非振荡放电过程能量转换关系示意图
(a)0< t< tm时的能量转换;(b)t > tm时的能量转换
当0< t< tm时,uC减小,i 增加,能量转换关系如图8-43(a)所示,电容释放能量,电感吸收并储存能量,电阻消耗能量;
当t > tm时,uC减小,i 减小,能量转换关系如图8-43(b)所示,电容、电感释放能量,电阻消耗能量。
2.欠阻尼条件——振荡放电过程
 为欠阻尼条件,即振荡放电过程,其特征根p1和p2是一对共轭复数,即
为欠阻尼条件,即振荡放电过程,其特征根p1和p2是一对共轭复数,即
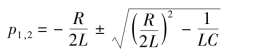
若δ 与ω 满足
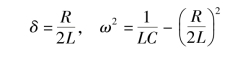
则
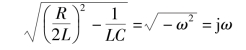
故特征根为
![]()
令![]() ,则
,则
![]()
ω0、ω 和δ的几何关系如图8-44 所示。
则
![]() (https://www.daowen.com)
(https://www.daowen.com)
根据
![]()
可求得
![]()
电容上的电压为
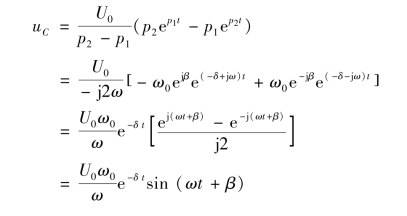
根据
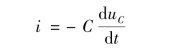
得
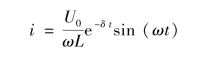
而电感电压为

从uC、i 和uL的表达式可以看出,它们的波形为衰减振荡状态,在整个过程中,它们将周期性地改变方向,储能元件也将周期性地交换能量。根据uC、i 和uL的表达式,可以得出如下结论。
(1)当ωt=kπ,k=0,1,2,…时,电流i 为零,即达到电压uC的极值点。
(2)当ωt=kπ+β,k=0,1,2,…时,电感电压uL为零,即达到电流i的极值点。
(3)当ωt=kπ-β,k=0,1,2,…时,电容电压uC为零。
在振荡放电的过程中,uC、i 和uL的波形如图8-45 所示。
根据零点划分的时域可以看出元件之间能量转换、吸收的情况,能量转换关系如图8-46 所示。

图8-46 振荡放电过程能量转换示意图
(a)0< ωt< β 时的能量转换;(b)β< ωt< π-β 时的能量转换;(c)x-β< ωt< π 时的能量转换
(1)当0< ωt< β 时,uC减小,i 增加,能量转换示意图如图8-46(a)所示,电容释放能量,电感吸收储存能量,电阻消耗能量;
(2)当β< ωt< π-β 时,uC减小,i 减小,能量转换示意图如图8-46(b)所示,电容释放能量,电感释放能量,电阻消耗能量;
(3)当π-β< ωt< π 时, 增加,i 减小,能量转换示意图如图8-46(c)所示,电感释放能量,电容储存能量,电阻消耗能量。
增加,i 减小,能量转换示意图如图8-46(c)所示,电感释放能量,电容储存能量,电阻消耗能量。
3.临界阻尼条件
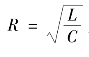 为临界阻尼条件,其特征方程的根是一对重实根,即
为临界阻尼条件,其特征方程的根是一对重实根,即
![]()
微分方程式的通解为
![]()
根据初始条件uC(0+)=U0,可得
![]()
根据条件![]() ,可得
,可得
![]()
即
![]()
所以电容电压为
![]()
电感电流为
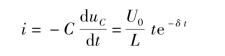
电感电压为
![]()
由此可知,uC、i、uL不做振荡变化,即具有非振荡的性质,其波形与图8-45 所示相似,求电流最大值可由![]() 决定,可求出此时tm=1/δ。
决定,可求出此时tm=1/δ。
这个过程是振荡与非振荡过程的分界线,所以 时的过渡过程称为临界非振荡过程,这时的电阻称为临界电阻。大于临界电阻的电路称为过阻尼电路,小于临界电阻的电路称为欠阻尼电路。
时的过渡过程称为临界非振荡过程,这时的电阻称为临界电阻。大于临界电阻的电路称为过阻尼电路,小于临界电阻的电路称为欠阻尼电路。
对二阶电路的分析,涉及决定二阶电路零输入响应特点的参数,即p1、p2、δ、ω0和ω。
p1、p2是微分方程的特征根,它直接决定了通解的形式,即决定二阶电路任何响应的自由分量的形式,又称为电路的固有频率,与电路的原始状态及激励均无关。
δ 为阻尼因子,ω 为衰减振荡角频率或阻尼振荡角频率。在R=0的理想情况下,当δ=0 时,为无阻尼情况,此时,![]() 称为无阻尼振荡角频率。在无阻尼条件下,各变量以ω0为角频率进行等幅正弦振荡,称为无阻尼振荡。
称为无阻尼振荡角频率。在无阻尼条件下,各变量以ω0为角频率进行等幅正弦振荡,称为无阻尼振荡。
【例8-14】 电路如图8-47 所示,已知US=5 V,C=1 μF,R=2 kΩ,L=1 H,开关S 原来闭合在触点1 处,在t=0 时,开关S 由触点1 接到触点2,求:
(1)uC、i、uL;
(2)imax。
解:(1)已知R=2 kΩ,而![]() ,所以
,所以![]() ,即该过程为临界非振荡过程。
,即该过程为临界非振荡过程。
初始条件为
![]()
特征根为
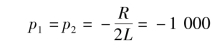
即
![]()
微分方程的通解为
![]()
根据初始条件可得
![]()
根据![]() ,可得
,可得
![]()
即
![]()
所以电容电压为
![]()
电感电流为
![]()
电感电压为
![]()
(2)电流的最大值由![]() 决定,即
决定,即
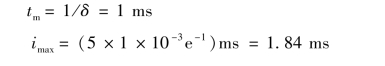
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





