动态电路在单位冲激函数的激励下所产生的零状态响应,称为冲激响应。
根据前面讨论的冲激函数δ(t)的定义和特性,当冲激函数作用于零状态的一阶RC 或RL 电路时,在[0-,0+]的区间内,它使电容电压或电感电流发生跃变。当t ≥0+时,冲激函数为零,但uC(0+)或iL(0+)不为零,电路中将产生相当于初始状态引起的零输入响应。因此,一阶电路冲激响应的求解关键在于冲激函数作用下的uC(0+)或iL(0+)的值。
RC 电路的冲激响应电路如图8-37(a)所示,RC 电路的激励是单位冲激电流源δi(t),求电容电压uC和电容电流iC零状态响应的过程如下。

图8-37 RC 电路的冲激响应及其等效电路
(a)RC 电路的冲激响应;(b)等效电路
根据KCL 有
![]()
而uC(0-)=0 。将式(8-36)在0-至0+的时间段内积分,得
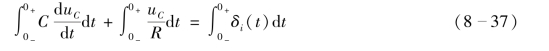
由式(8-36)可知,uC发生跃变但为有限值。若uC为冲激函数,则![]() 就为冲激函数的一阶导数,这样就不能满足KCL,即式(8-36)将不能成立,因此,uC不可能是冲激函数,即式(8-37)左边第二个积分项为零。从而可推出
就为冲激函数的一阶导数,这样就不能满足KCL,即式(8-36)将不能成立,因此,uC不可能是冲激函数,即式(8-37)左边第二个积分项为零。从而可推出
![]()
将uC(0-)=0 代入可得到
![]()
电路时间常数τ=RC,当t ≥0+时,冲激电流源相当于开路,等效电路如图8-37(b)所示,电路中产生的是零输入响应,这时的电容电压为
![]()
RL 电路的冲激响应如图8-38(a)所示。
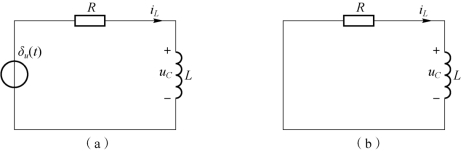
图8-38 RL 电路的冲激响应及其等效电路
(a)RL 电路冲激响应;(b)等效电路
RL 电路在t ≥0-时的单位冲激电压δu(t)激励下的零状态响应为
![]()
而在t ≥0+时表达式为
![]()
由于电感电流在t=0 时发生跃变,所以电感电压为(https://www.daowen.com)
![]()
iL、uL的波形如图8-39 所示,t=0-到0+电感电流iL发生跃变,电感电压uL发生冲激。
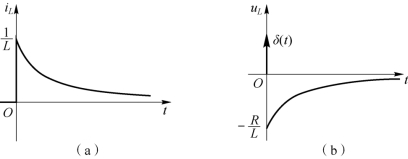
图8-39 RL 电路冲激响应下的波形图
(a)iL的波形图;(b)uL的波形图
因为单位冲激函数δ(t)和单位阶跃函数ε(t)具有微分关系,即
![]()
故根据线性关系,单位冲激响应h(t)和单位阶跃响应s(t)也具有微分关系,即
![]()
【例8-13】 电路如图8-40 所示,已知uC(0-)=0 ,求当iS(t)为单位冲激函数时的冲激响应uC(t)和iC(t)。
解:先求出当iS(t)=ε(t)时的单位阶跃响应
时间常数为
![]()
所以电容电压的单位阶跃响应为零状态响应,即
![]()
再求当iS=δ(t)时的单位冲激响应,通过对电容电压单位阶跃响应函数求微分得到,即
![]()
上式中第二项δ(t)只有在t=0 时不为零,即
![]()
而当t=0 时,![]() ,所以此项为零,因此有电容电压的单位冲激响应为
,所以此项为零,因此有电容电压的单位冲激响应为
![]()
电容电流的单位冲激响应可以通过对电容电压微分求得,即
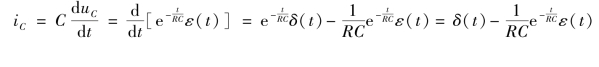
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





