冲激函数的演变如图8-36 所示。

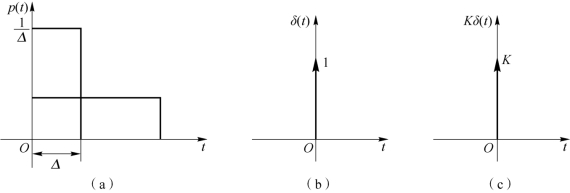
图8-36　冲激函数的演变

（a）单位矩形脉冲；（b）单位冲激函数；（c）冲激函数

图8-36（a）所示为单位矩形脉冲p（t），脉冲宽度为Δ，高度为，矩形面积为Δ·，在保持矩形面积不变的情况下，当它的宽度越来越窄时，它的高度会越来越大，当脉冲宽度Δ→0 时，脉冲高度，这样就可以得到一个宽度为零、幅度为无限大但面积仍为1的脉冲函数波形δ（t），如图8-36（b）所示，这个函数就是单位冲激函数。因此，单位冲激函数δ（t）定义为

单位冲激函数δ（t）在t ≠0 处为零，但在t＝0 处为不连续的。

注意：

在图8-36（b）所示的单位冲激函数波形中，箭头旁边的1 不是表示脉冲的高度，而是表示脉冲的面积。冲激函数对电路的作用取决于它的面积，面积为K的冲激函数可表示为Kδ（t），K 为冲激函数的强度，如图8-36（c）所示。

与在时间上延迟的单位阶跃函数一样，可以把发生在t＝t0时的单位冲激函数写为δ（tt0），若强度为K，则可以表示为Kδ（t－t0）。

冲激函数有如下两个性质。

（1）单位冲激函数δ（t）对时间的积分等于单位阶跃函数ε（t），即

反之，阶跃函数ε（t）对时间的一阶导数等于单位冲激函数δ（t），即

（2）单位冲激函数具有筛分性质。因为当t ≠0 时，δ（t）＝0 ，所以对任意在t＝0 时连续的函数f（t），有(www.daowen.com)

则

同理，对于任意在t＝t0时连续的函数f（t），有

冲激函数有将一个函数在某个时刻的值筛分出来的本领，筛分性质又称为取样性质。

【例8-12】　试求的值。

解：应用冲激函数的筛分性质，原式可写为

单位冲激函数f（t）是英国物理学家狄拉克在研究量子力学时提出的，因此，f（t）又称为狄拉克函数，该函数可以用于描述某些作用时间极短，数值极大且效果有限的物理现象，如电路中的瞬时充电现象。

当把一个单位冲激电流δi（t）（其单位为A）加到初始电压为零，且C＝1 F的电容上时，电容电压为

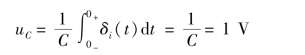
该式表明，单位冲激电流δi（t）瞬时把电荷转移到电容上，使得电容电压从零跃变到1 V。

同理，如果把一个单位冲激电压δu（t）（其单位为V）加到初始电流为零，且L＝1 H的电感上，则电感电流为

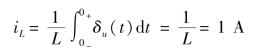
该式表明，单位冲激电压δu（t）瞬时在电感内建立了1 A的电流，使得电感电流从零跃变到1 A。