微分电路和积分电路是矩形脉冲激励下的RC 电路。若选取不同的时间常数，则可构成输出电压波形与输入电压波形之间的特定（微分或积分）的关系。

RC 电路如图8-34（a）所示，输入电压为图8-34（b）所示的方波脉冲。

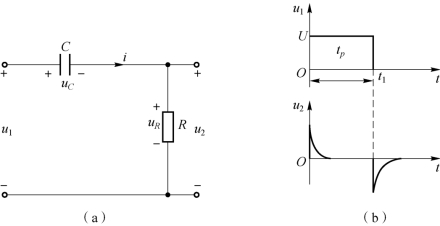
图8-34　微分电路及其相应波形

（a）RC 电路；（b）相应波形

输出电压u2从电阻R 两端输出，RC 电路时间常数远远小于输入电压脉冲宽度，即

在0< t< tp期间，电容充电，应用三要素法得

此时电容上电压大小与时间常数τ＝RC 有关，当时间常数τ＝RC ≪tp时，电容很快充电到U1。当t＝tp时，输入电压u1突然降为零，这相当于输入端短路，电容经电阻放电，则在t＝tp时，u2（tp）＝－uC＝－U1，所以在t > tp的放电过程中有

从而在τ ≪tp的条件下，输出电压u2就是尖脉冲，如图8-34（b）所示。在数字电路中，尖脉冲常常作为触发信号。

此种RC 电路又称为微分电路，原因如下。

根据KVL 定律，有

当R 很小时，u1≈uC所以输出电压为

式（8-31）中输出电压与输入电压成微分关系，所以一般将这种RC 电路称为微分电路。需要指出，这种微分电路是近似的，因为只有在RC 很小时，u2（t）≈0 时才与u1（t）有微分关系，而输出电压u2（t）≈0 已无实际意义，但如果接入到集成运算放大器上，微分电路的性能将大大提高。

RC 电路如图8-35（a）所示，输入电压为图8-35（b）所示的方波脉冲。(www.daowen.com)

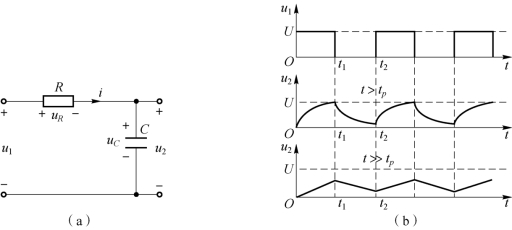
图8-35　积分电路及其响应波形

（a）积分电路；（b）响应波形

输出电压u2从电容C 两端输出，RC 电路时间常数远远大于输入电压脉冲宽度，即

如图8-35（a）所示电路，在0< t< tp期间，电容充电且电容两端电压为零状态响应，即

若取τ ≫tp，电容充电过程非常慢，则在t＝tp时，电容上的电压值远小于U1。

设此时的电压值为U0，则在t > tp时，电容放电，即

在此RC 电路中，因为

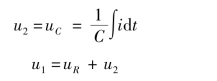
当u2＝uC≈0 时，有

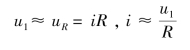
则

式（8-32）表明，当RC 很大，且输出电压uC≈0 时，输出电压与输入电压成积分关系，所以一般将这种RC 电路称为积分电路。但需注意，在真正有输出时，输出电压与输入电压之间不存在积分关系。如果接入到集成运算放大器上，积分电路可以应用在工程电路中。

积分电路的输出波形如图8-35（b）所示，当选择电路的时间常数较大时，电容电压周期的充电放电，能够得到较好的锯齿波信号，锯齿波信号应用在电视机和示波器中的扫描中；当时间常数τ ≫tp时，满足积分电路条件，电容电压输出三角形波形，幅度较小，但可以实现波形变换或正弦信号的移相。