RL 零状态响应电路如图8-15 所示。

电路在开关闭合前为零初始状态，即电感电流为

开关闭合后，根据KVL 有

电感的伏安特性为

代入上式得到微分方程，即

与RC 电路分析相类似，该方程仍为一阶线性常系数非齐次微分方程，方程的解由非齐次方程的特解（稳态分量）和对应的齐次方程的通解（暂态分量）两个分量组成，即

特解是换路后的稳态分量，这时

即

齐次方程的通解为

所以有

将初始条件代入确定系数A，可得

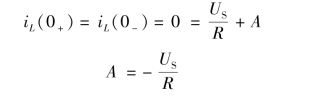
则(www.daowen.com)

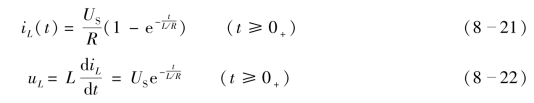
RL 电路的零状态响应曲线如图8-16 所示。

图8-16　RL 电路零状态响应曲线

（a）iL的波形图；（b）uL的波形图

【例8-6】　电路如图8-17（a）所示，换路前电路已经处于稳定状态，在t＝0 时开关S 打开，求t>0 后iL和uL的变化规律。

解：这是一个RL 电路零状态响应问题，t>0 后的等效电路如图8-17（b）所示，注意图（a）中的RS在换路后与理想电流源串联，对外电路不起作用，故

时间常数为

图8-17　例8-6 图

（a）电路图；（b）等效电路图

换路后的电感电流的稳态解为

所以电感电流的零状态响应为

电感两端电压的零状态响应为

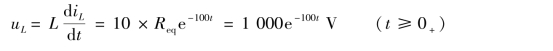
注意：

在t＝0＋时刻，电感元件两端会出现瞬间高压。在电力系统中，感性元件较多，换路时应采取必要的措施避免出现瞬间高电压，对元件或工作人员造成危害。