RC 电路的零状态响应如图8-13 所示。

图8-13 中电路在开关闭合前处于零初始状态，即

当开关闭合后，根据KVL 有

电容伏安特性为

代入上式得到微分方程，即

该方程为一阶线性常系数非齐次微分方程，方程的解由非齐次方程的特解u′C和对应的齐次方程的通解u″C两个分量组成，即

特解为换路后电路又达到稳定状态的解，这时

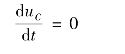
即

由于特解与输入激励的变化规律有关，因此称为强制分量，周期性激励时强制分量为电路的稳态解，因此又称为稳态分量。

而齐次方程的通解为

通解变化规律由电路结构和参数有关，常称为自由分量，而通解又随时间增大衰减为零，因此也称为暂态分量。

故方程的解为

(www.daowen.com)

将初始值uC（0＋）＝uC（0－）＝0 代入，可求得

因此求得零状态响应为

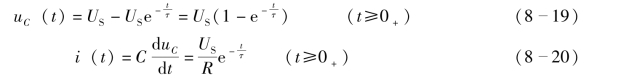
RC 电路的零状态响应曲线如图8-14 所示。

从式（8-19）和（8-20）可以得出以下结论。

（1）电压、电流是随时间按同一指数规律变化的函数，电容电压由稳态分量（强制分量）和暂态分量（自由分量）两部分构成，各分量的波形及叠加结果如图8-14（a）所示，电流波形如图8-14（b）所示。

（2）响应变化的快慢由时间常数τ 决定，τ 越大充电越慢，τ 越小，充电越快。

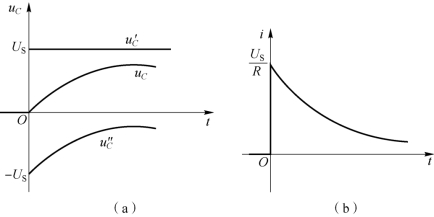
图8-14　RC 电路的零状态响应曲线

（a）uC的波形图；（b）i的波形图

（3）响应与外加激励呈线性关系。

（4）充电过程的能量关系如下：

电容最终储存能量为

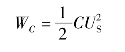
电源提供的能量为

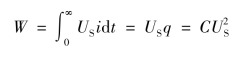
电阻消耗的能量

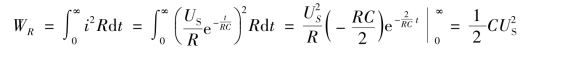
可见，不论电路中电容C 和电阻R的数值为多少，在充电过程中，电源提供的能量只有一半转变成电场能量储存于电容中，另一半则被电阻所消耗，故充电效率只有50%。