分析动态电路的首要任务就是建立描述电路的方程，常采用是时域分析法。根据KCL、KVL 和动态元件的伏安特性关系（VCR）建立描述电路的线性常系数微分方程，然后求解，从而得到电路中所求的变量（电压或电流）。时域分析法也称为经典法。

下面以RC 电路和RLC 电路为例，给出动态电路的方程描述方法。

图8-1（a）所示为RC 电路，根据KVL 列出回路电压方程，即

图8-1　RC 电路和RLC 电路图

（a）RC 电路；（b）RLC 电路

电容元件的VCR 为

代入电压方程，可以得到以电容电压为变量的电路方程，即

式（8-1）是以uC为变量的常系数线性一阶微分方程，微分方程为一阶的电路称为一阶电路。

图8-1（b）所示电路是RLC 电路，根据KVL 列出回路电压方程，即(www.daowen.com)

电容元件、电感元件的VCR 为

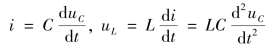
代入电压方程，可以得到以电容电压为变量的二阶微分方程为

式（8-2）是以uC为变量的常系数线性二阶微分方程，微分方程为二阶的电路称为二阶电路。

因此动态电路可总结如下。

（1）描述动态电路的电路方程为微分方程。

（2）动态电路微分方程的阶数等于电路中动态元件的个数，用n 阶微分方程描述的动态电路称为n 阶电路。

描述n 阶动态电路的微分方程的一般形式为

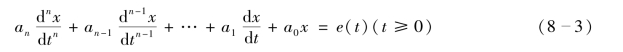
式（8－3）中的系数由动态电路的网络结构和元件参数决定。在求解微分方程时，微分方程的解由通解和特解构成，特解的求取需要变量的初始值，动态电路的微分方程常以电容电压uC或电感电流iL为变量。因此，相应的微分方程的初始条件为电容电压或电感电流的初始值。