图7-23 所示为一线性二端口,各电压、电流用相量法表示,也可以用瞬时值、运算法表示,各端子的电流、电压参考方向如图所示。
1.阻抗方程和Z 参数
如果两个端口电流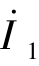 和
和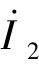 已知,可以利用替代定理将两个端口的电流
已知,可以利用替代定理将两个端口的电流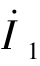 和
和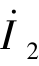 看作是外施的独立电流源。根据叠加定理,
看作是外施的独立电流源。根据叠加定理,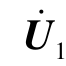 和
和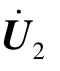 等于各个电流源单独作用时产生的电压之和,即
等于各个电流源单独作用时产生的电压之和,即

式(7-20)为阻抗方程,也称为二端口网络的Z 参数方程,式中的Z11、Z12、Z21、Z22称为二端口网络的Z 参数,它们都具有阻抗的量纲。式(7-20)也可以写成矩阵形式,即
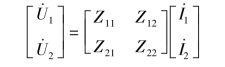
上式中的系数矩阵称为Z 参数矩阵,记为Z。Z11、Z12、Z21、Z22可以用下述方法计算或试验测量求得。
令端口2-2′开路,即电流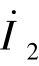 =0,在端口1-1′施加电流源
=0,在端口1-1′施加电流源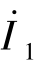 ,如图7-24(a)所示。由式(7-20)可得
,如图7-24(a)所示。由式(7-20)可得


式(7-21)中,Z11为端口2-2′开路时端口1-1′的输入阻抗;式(7-22)中,Z21为端口2-2′开路时端口1-1′转移到端口2-2′的转移阻抗。
同理,令端口1-1′开路, =0,在端口2-2′处施加电流源
=0,在端口2-2′处施加电流源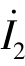 ,如图7-24(b)所示,由式(7-20)可得
,如图7-24(b)所示,由式(7-20)可得

式(7-23)中,Z12为端口1-1′开路时端口2-2′转移到端口1-1′的转移阻抗;式(7-24)中,Z22为端口1-1′开路时端口2-2′的输入阻抗。
由于Z 参数都是在一个端口开路的情况下计算或测试得到,所以Z 参数也称为开路阻抗参数。
【例7-5】 求图7-25(a)所示T 形二端口网络的Z 参数,设Z1、Z2和Z3都为已知。
解:用以下两种方法求解。
方法一:应用试验测量法。
根据式(7-21)和式(7-22)求得端口1-1′的输入阻抗和转移阻抗分别为
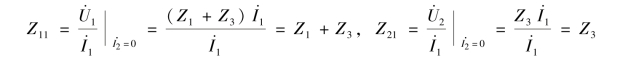
根据式(7-23)和式(7-24)求得转移阻抗和端口2-2′的输入阻抗分别为
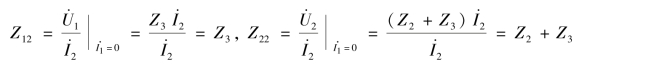
于是得到Z 参数矩阵为
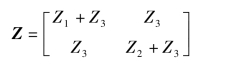
方法二:用网孔电流法列方程。
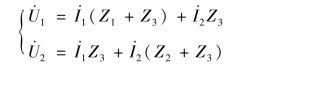
于是得到Z 参数矩阵为
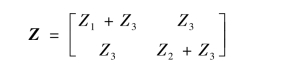
比较两种解法,对于T 形电路求Z 参数,应用网孔电流法直接列方程求解比较简单,如果电路中含有受控源,则这种方法的优点会更加突出。
由本例结果可知,Z12=Z21=Z3,Z 参数中只有3 个是独立的。对于由线性R、L(M)、C 元件所组成的任意无源二端口网络来说,根据互易定理,可证明Z12=Z21总是成立的,这种不含受控源的二端口网络被称为互易二端口网络。
如果一个二端口网络的Z 参数,除了Z12=Z21外,还有Z11=Z22,则此二端口网络的两个端口1-1′和2-2′互换位置后与外电路连接,其外部特性不会有任何变化,即这种二端口从任一端口看进去,它的电气特性是一样的,因而称为电气对称,二端口网络也被称为对称二端口网络。结构上对称的不含受控源的二端口网络是对称二端口网络,但是电气上对称并不一定意味着结构上的对称。显然对于对称二端口网络的Z 参数,只有2 个参数是独立的。
【例7-6】 求图7-26 所示二端口网络的Z 参数。
解:应用网孔电流法求解。
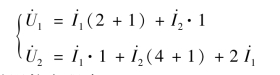
整理后,得到二端口网络的阻抗方程为
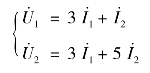
于是得到Z 参数矩阵为
![]()
由计算结果可知,此二端口网络的Z 参数Z12≠Z21,Z11≠Z22。对于含受控源的线性R、L(M)、C 二端口网络,利用特勒根定理可以证明互易定理一般不成立,阻抗参数不对称,4 个参数相互独立。
2.导纳方程和Y 参数
对图7-23 所示的二端口网络,假设两个端口电压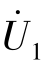 和
和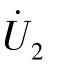 已知,可以利用替代定理把两个端口电压
已知,可以利用替代定理把两个端口电压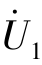 和
和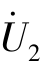 都看作是外加的独立电压源。根据叠加定理,
都看作是外加的独立电压源。根据叠加定理,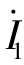 和
和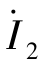 等于各个独立电压源单独作用时产生的电流之和,即
等于各个独立电压源单独作用时产生的电流之和,即

式(7-25)可以写成矩阵形式,即
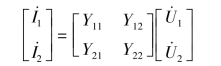
上式中的系数矩阵称为Y 参数矩阵,记为Y。Y11、Y12、Y21、Y22具有导纳性质,可以用下述方法计算或试验测量求得,如图7-27 所示。
令端口2-2′短路,即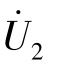 =0,在端口1-1′施加电压源
=0,在端口1-1′施加电压源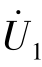 ,如图7-27(a)所示,由式(7-25)得
,如图7-27(a)所示,由式(7-25)得

式(7-26)中,Y11为端口2-2′短路时端口1-1′的输入导纳;式(7-27)中,Y21为端口2-2′短路时端口1-1′转移到端口2-2′的转移导纳。
同理,令端口1-1′短路,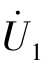 =0,在端口2-2′施加电压源
=0,在端口2-2′施加电压源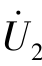 ,如图7-27(b)所示,由式(7-25)可得
,如图7-27(b)所示,由式(7-25)可得

式(7-28)中,Y12为端口1-1′短路时端口2-2′转移到端口1-1′的转移导纳;式(7-29)中,Y22为端口1-1′短路时端口2-2′的输入导纳。
由于Y 参数都是在一个端口短路的情况下计算或测试得到,所以Y 参数也称为短路导纳参数。
与阻抗参数类似,互易二端口网络的Y 参数满足Y12=Y21。对称二端网络,除了满足Y12=Y21外,还满足Y11=Y22的条件。对于含受控源的线性R、L(M)、C的二端口网络,利用特勒根定理可以证明互易定理一般不成立,导纳参数也不对称,4 个参数相互独立。
开路阻抗矩阵Z 与短路导纳矩阵Y 之间存在互逆的关系,即
![]()
【例7-7】 求图7-28(a)所示二端口的Y 参数。
解:这个二端口网络是一个典型的π 形电路。本例应用短路试验测定法计算短路导纳。(https://www.daowen.com)
端口2-2′短路,在端口1-1′外施加电压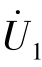 ,如图7-28(b)所示,可求得
,如图7-28(b)所示,可求得
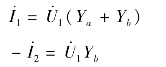
根据实验测定法可求得
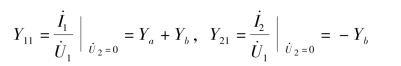
同样,将端口1-1′短路,在端口2-2′上外施加电压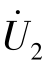 ,如图7-28(c)所示,则可得
,如图7-28(c)所示,则可得
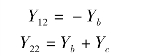
由本例计算结果可知,互易二端口网络的Y 参数满足Y12=Y21。
对于一个π 形二端口网络,应用结点电压法比较容易列出导纳方程,比短路试验法简单,如果电路是含有线性受控源的π 形二端口网络,则结点电压法的优点会更加突出。
【例7-8】 求如图7-29 所示二端口网络的Y 参数。
解:应用结点电压法列方程,即
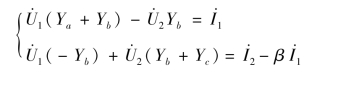
整理成导纳方程,即
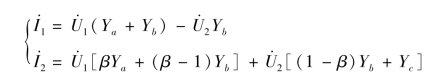
可得到Y 参数矩阵为
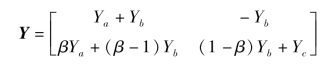
当然也可以应用短路试验测试法计算,但由于含有受控源,求解过程较为烦琐。
本例中含有受控源,不是互易网络,Y 参数Y12≠Y21。
Y 参数和Z 参数都可以描述一个二端口网络的端口外特性。如果是T 形网络,则先求Z参数比较容易;如果是π 型网络,则先求Y 参数比较容易,然后可以应用式(7-30)表示的互逆关系求出另外一个参数。对于一些特殊的二端口网络,有的只有Z 参数,没有Y 参数,如图7-30(a)所示。也有的二端口网络没有Z 参数,只有Y 参数,如图7-30(b)所示。还有的二端口网络Z 参数和Y 参数都没有。这就意味着某些二端口网络可以用除Z参数和Y 参数以外的其他形式的参数描述其端口外特性。
3.混合方程和H 参数
对于图7-23 所示的二端口网络,如果在其两个端口分别施加一个电流源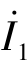 和一个电压源
和一个电压源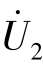 ,则根据叠加定理,
,则根据叠加定理,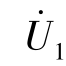 和
和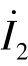 应等于电流源
应等于电流源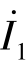 和电压源
和电压源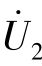 单独作用时所产生的电压和电流之和,即
单独作用时所产生的电压和电流之和,即

式(7-31)称为混合方程,又称为二端口网络的H 参数方程。其中,H11、H12、H21、H22称为二端口网络的混合参数或H 参数。H 参数在晶体管电路中获得广泛应用。
式(7-31)也可以写成矩阵形式,即
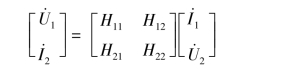
其中,系数矩阵称为混合参数矩阵,记为H。H11、H12、H21、H22可按试验测定方法计算或测试得到,即
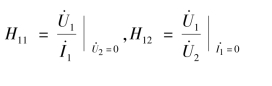
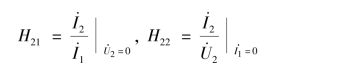
可见H11和H21有短路参数的性质,H12和H22有开路参数的性质。也不难看出![]() ,H22=
,H22=![]() 。H11具有电阻的量纲,H22具有电导的量纲,H12和H21分别为电压比和电流比,无量纲。当然也可以根据网络列出H 参数方程来求得H 参数。对于互易二端口网络有H21=-H12,对于对称的二端口网络,由于Y11=Y22或Z11=Z22,则有H11H22-H12H21=1。
。H11具有电阻的量纲,H22具有电导的量纲,H12和H21分别为电压比和电流比,无量纲。当然也可以根据网络列出H 参数方程来求得H 参数。对于互易二端口网络有H21=-H12,对于对称的二端口网络,由于Y11=Y22或Z11=Z22,则有H11H22-H12H21=1。
【例7-9】 图7-31 为一只晶体管的小信号工作条件下的简化等效电路,求其H 参数。
解:该电路的混合方程为
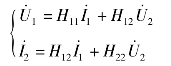
该电路满足的电压电流关系为
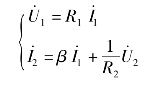
所以H 参数矩阵为
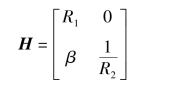
4.传输方程和T 参数
在电力和电信传输中,分析如图7-23 所示的二端口网络时常用传输方程,即

需要注意的是二端口网络中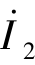 的参考方向和式(7-32)中
的参考方向和式(7-32)中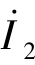 前的负号。
前的负号。
式(7-32),也可以写成矩阵形式,即
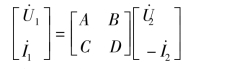
其中,A、B、C、D 称为T 参数。T 参数的求取可以根据二端口网络列出方程式(7-32),
也可以应用开路短路测试法求取,即
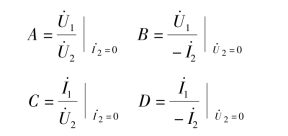
上式中,A、B、C、D 分别反映两个端口之间电压、电流关系,因而都具有转移性质,其中A 和D 分别是电压比和电流比,无量纲,B 为电阻的量纲,C 为电导的量纲。
对于互易二端口网络,可以证明AD-BC=1,对称二端口网络T 参数还满足A=D。
【例7-10】 如图7-32 所示理想变压器,求其T 参数。
解:图7-32 所示电路的端口特性为
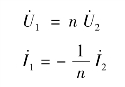
所以T 参数矩阵为
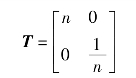
如果已知二端口网络的某种参数,可以经过方程变换求出其他参数。表7-1 列出了4种参数之间的换算关系,以备查用。
表7-1 二端口网络4 种参数之间的关系
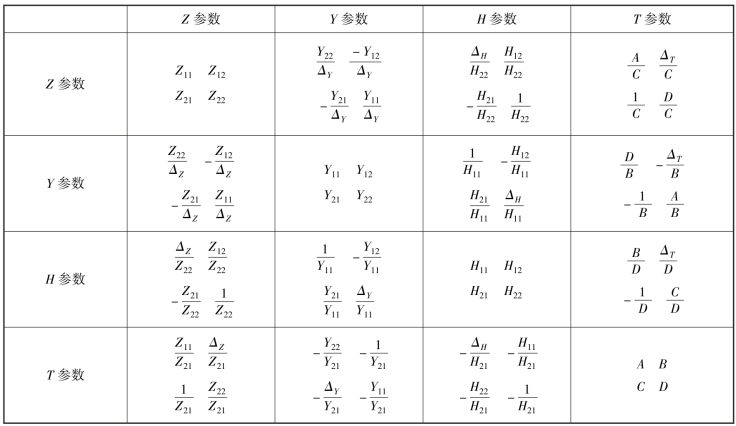
在表7-1 中,ΔZ、ΔY、ΔH和ΔT为
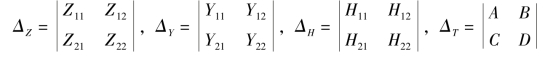
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






