含有耦合的电感在特定的连接方式下可以通过去耦等效进行化简，去耦等效的方法需要根据耦合电感的连接方式来定，耦合电感的连接方式有顺向串联、反向串联、同侧并联、异侧并联、同名端为共端的T 形连接和异名端为共端的T 形连接。

1.串联耦合电感的去耦等效

1）顺向（接）串联

图7-7（a）所示电路为耦合电感的串联电路，电流都是从互感线圈的同名端流入，它们产生的磁场是相互增强的，称为顺向串联。

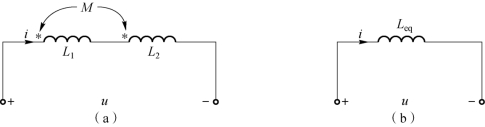
图7-7　顺向串联互感线圈的去耦等效

（a）顺向串联互感线圈；（b）去耦等效

按图7-7（a）示电压、电流的参考方向，KVL 方程为

根据式（7-4）可以得到图7-5（b）所示的去耦后的无互感等效电路，其等效电感为

2）反向（接）串联

图7-8（a）所示的耦合电感的串联电路，电流从一个互感线圈的同名端流入，从另一个互感线圈的同名端流出，它们产生的磁场是相互削弱的，称为反向串联。

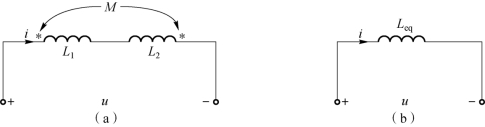
图7-8　反向串联互感线圈的去耦等效

（a）反向串联互感线圈；（b）去耦等效

按图7-8（a）所示电压、电流的参考方向，KVL 方程为

根据式（7-5）可以给出图7-8（b）所示去耦后的无互感等效电路。等效电路的参数为

互感线圈串联后的等效电路仍呈感性，即

可以推出，即互感系数不大于两个自感系数的算术平均值。

另外，测量互感系数的方法：把两互感线圈顺接一次，得到等效电感L顺，然后再反接一次，得到等效电感L反，其互感系数为

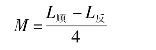
2.并联耦合电感的去耦等效

1）同侧并联

图7-9（a）为耦合电感的并联电路，其同名端连接在同一个结点上，称为同侧并联。根据KVL 可以得到同侧并联电路的方程为

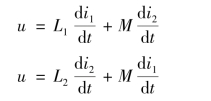
由于i＝i1＋i2，联立求解得到端口电压u 和端口电流i的关系为

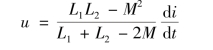
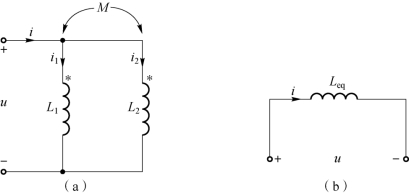
图7-9　同侧并联互感线圈的去耦等效

（a）同侧并联互感线圈；（b）去耦等效

根据上述方程可以得到去耦后的无互感等效电路，如图7-9（b）所示，其等效电感为

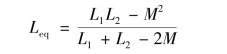
2）异侧并联(www.daowen.com)

在图7-10（a）中，耦合电感的异名端连接在同一个结点上，称为异侧并联。

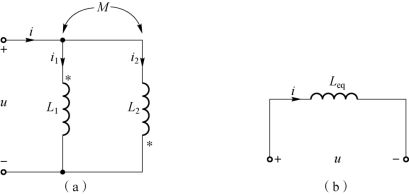
图7-10　异侧并联互感线圈的去耦等效

（a）异侧并联互感线圈；（b）去耦等效

根据KVL 可以得到异侧并联电路的方程为

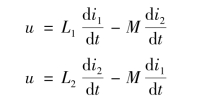
由于i＝i1＋i2，联立求解得到端口电压u 和端口电流i的关系，即

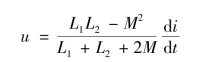
根据上述方程可以得到去耦后的无互感等效电路，如图7-10（b）所示，其等效电感为

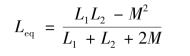
3.T 形连接耦合电感的去耦等效

如果耦合电感的2 条支路各有一端与第3 条支路形成一个仅含3 条支路的共同结点，则称为耦合电感的T 形连接。显然耦合电感的并联也属于T 形连接。

1）同名端为共端的T 形连接

图7-11（a）所示电路为同名端为共端的T 形连接。

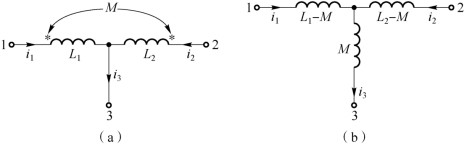
图7-11　同名端为共端互感线圈的去耦等效

（a）同名端为共端互感线圈；（b）去耦等效

根据图7-11（a）中所标电压、电流的参考方向可得

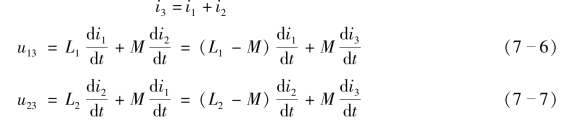
根据式（7-6）和式（7-7）可得到去耦后的无互感等效电路，如图7-11（b）所示。

2）异名端为共端的T 形连接

图7-12（a）所示的电路为异名端为共端的T 形连接。

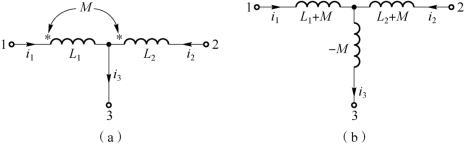
图7-12　异名端为共端互感线圈的去耦等效

（a）异名端为共端互感线圈；（b）去耦等效

根据图7-12（a）所标电压、电流的参考方向得

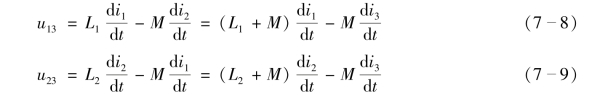
根据式（7-8）和式（7-9）可以得到去耦后的无互感等效电路，如图7-12（b）所示。

4.受控源等效电路

如图7-13（a）所示电路，列写两个线圈的端口电压u 和端口电流i 方程为

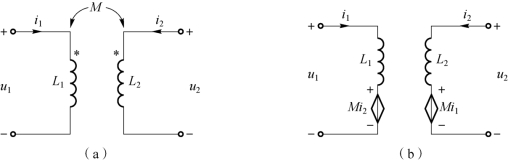
图7-13　互感线圈的受控源去耦等效

（a）互感线圈；（b）受控源去耦等效

其中，式（7-10）中的项可以看作是由电流i2控制的电压源，式（7-11）中的项可以看作是由电流i1控制的电压源，因此其去耦后的无互感等效电路为图7-13（b）所示。