1.串联谐振的条件

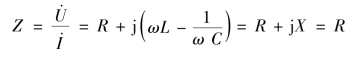
如图6-5 所示的RLC 串联谐振电路，根据谐振定义，端口输入阻抗为即谐振时电路呈纯电阻性。此时，输入阻抗虚部为0，可以得到RLC 串联电路的谐振条件，即

即串联谐振时，感抗等于容抗，ρ 为串联谐振电路的特性阻抗，从而可得

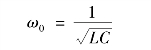
或

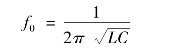
ω0称为RLC 串联谐振电路的谐振角频率，f0称为RLC 串联谐振电路的谐振频率，它们是由电路的参数决定的。因此，ω0也称为固有角频率，f0称为固有频率。

通过以上分析可知，改变电源的频率使其与电路的固有频率相等，或改变电路中电感（电容）的参数使其与电源频率相等，都可以使电路发生谐振。无线收音机在接收电台信号时是通过调节可变电容使电路的固有频率等于某一电台的发射频率来实现谐振的。

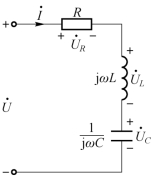
图6-5　RLC 串联谐振

2.串联谐振的特点

根据谐振定义及以上分析，可知串联谐振的特点如下。

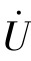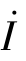（1）谐振时电路端口电压和端口电流同相位。

（2）谐振时输入阻抗Z＝R 为纯电阻，阻抗模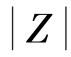与角频率ω 之间的关系如图6-6 所示，由图可知串联谐振时阻抗模最小。端口电流I 与角频率ω的关系如图6-7 所示，由图可知串联谐振时电路中的电流达到最大，该结论也作为判断谐振的依据。

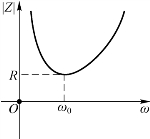
图6-6　串联谐振阻抗模与角频率的关系

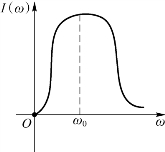
图6-7　串联谐振电流与角频率的关系

（3）谐振时的电压为

其中，Q 为品质因数，用来表示谐振电路的性质。

品质因数是指谐振时，感抗或容抗消耗的无功功率与电阻消耗的有功功率的比值。工程上通常用特性阻抗与电阻的比值表示，即(www.daowen.com)

当电路的品质因数大于或等于10 时，称为高Q 值电路，通常应用在通信系统中。谐振电路通常工作在谐振频率或者其临近的频率。

式（6-12）表明谐振时电感和电容电压大小相等，相位相反，相量如图6-8 所示，串联总电压，LC 串联在一起相当于短路，所以串联谐振也称为电压谐振，此时，电源电压全部加在电阻上，即

图6-8　串联谐振各元件电压相量

从式（6-10）、式（6-11）可知，如果Q>1，则UL＝UC>U，当Q>>1 时，电感和电容两端的电压大大高于电源电压U，称为过电压现象。在工程应用中，当电信号微弱时，可以通过电压谐振获得一个较高的电压。另外，在电力系统中如果出现电压谐振，过高的电压会使电感线圈和电容器的绝缘被击穿，因此应尽可能地避免谐振。

（4）谐振时的有功功率为

谐振时电阻消耗的功率最大。谐振时的无功功率为

谐振时电源不向电路输送无功功率，电感中的无功与电容中的无功功率大小相等，互相补偿，彼此进行能量交换，如图6-9 所示。

【例6-4】　某收音机的输入回路如图6-10 所示，L＝0.3 mH，R＝10 Ω，为收到中央电台f0＝2MHz的信号，（1）求调谐电容C；（2）如果输入电压为US＝1 mV，求谐振电流I0和此时的电容电压UC；（3）求品质因数Q。

解：①由串联谐振的条件可得

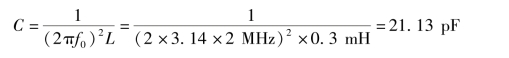
②由于串联谐振时，总阻抗Z＝R，则谐振电流为

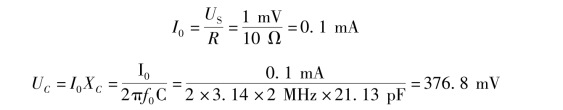
③品质因数为

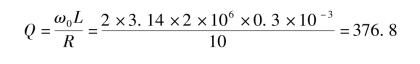
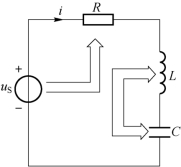
图6-9　串联谐振功率之间的关系

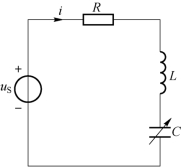
图6-10　某收音机的输入回路