第4 章讨论的周期信号有效值的定义,对于非正弦周期信号仍然适用,即非正弦周期信号的有效值也等于其方均根值。
设非正弦周期电流为
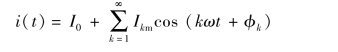
根据有效值的定义,即
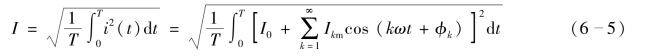
利用三角函数相关的性质,可推导出非正弦周期电流的有效值为
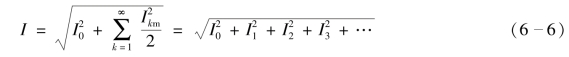
式(6-6)中,I0为直流分量,I1、I2、I3分别为基波、二次谐波、三次谐波的有效值。
同理,可得到非正弦周期电压信号u的有效值为
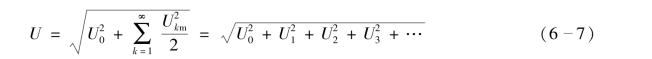
非正弦周期函数的有效值为直流分量及各次谐波分量有效值平方和的方根。在实际测量过程中还会用到真有效值。真有效值的定义及测量见二维码6-1。

二维码6-1 真有效值的定义及测量
另外,在实际的电工电子测量过程中也会用到平均值的概念,工程上把非正弦周期电流的平均值定义为
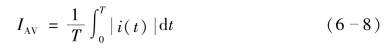
即非正弦周期电流的平均值等于此电流绝对值的平均值。
由于不同类型测量仪表的读数表示的含义不同,故非正弦周期信号在测量时需要选择合适的仪表。例如,非正弦周期信号有效值的测量要使用电磁系或电动系仪表,非正弦周期信号平均值的测量要使用磁电系仪表。
在如图6-4 所示的二端网络中,端口电压u(t)与端口电流i(t)分别为非正弦周期信号,u(t)与i(t)取关联参考方向。
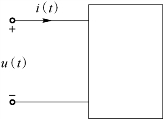
图6-4 非正弦信号作用的二端网络
![]()
代入电压、电流的表达式并利用三角函数的性质,可得
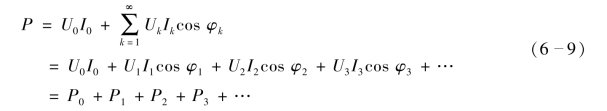
即非正弦周期电流电路的平均功率为直流分量的功率和各次谐波的平均功率之和,不同频率的信号不产生平均功率。
【例6-3】 已知如图电路6-4 所示二端网络的端口电压、端口电流分别为
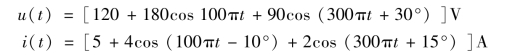 (www.daowen.com)
(www.daowen.com)
计算电压u(t)、电流i(t)的有效值和二端网络吸收的平均功率。
解:根据电压表达式可知电压u(t)的直流分量为
![]()
基波分量为
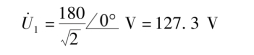
三次谐波分量为
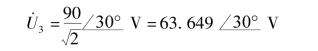
根据电流表达式可知电流i(t)直流分量为
![]()
基波分量为
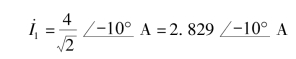
三次谐波分量为
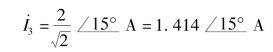
电压u(t)的有效值为
![]()
电流i(t)的有效值为
![]()
直流量作用时对应的平均功率为
![]()
基波作用时对应的平均功率为
![]()
三次谐波波作用时对应的平均功率为
![]()
二端网络吸收的平均功率为
![]()
从例6-3的分析结果可知,非正弦周期信号的主要能量集中在低频部分,高频部分的能量很小,因此,在分析计算时可以只取部分低频信号进行分析。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

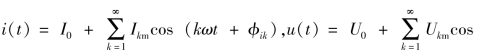 (kωt+φ
(kωt+φ





