非正弦周期电流、电压信号作用下的线性电路的稳态分析通常采用谐波分析法。谐波分析法实质上就是通过应用傅里叶级数展开式,将非正弦周期信号分解为直流量和一系列不同频率的正弦量之和,再根据线性电路的叠加定理,分别计算在直流量作用下和各个正弦量单独作用下电路中产生的电流分量和电压分量,最后,把所得分量按时域形式叠加从而得到电路在非正弦周期激励下的稳态电流和电压。
根据以上讨论可得非正弦周期电流电路的计算步骤如下:
(1)把给定电源的非正弦周期电流或电压进行傅里叶级数分解,将非正弦周期电流或电压信号展开成直流量和多个频率的正弦信号的叠加;
(2)利用直流和正弦交流电路的计算方法,对直流量和各次谐波激励分别计算其响应,并画出对应的等效电路;
(3)将以上计算结果转换为瞬时值进行叠加。
注意:
①当直流量单独作用时,电路中电感相当于短路、电容相当于开路。
②傅里叶级数展开式中的各次谐波(多个频率的正弦)电路的计算采用相量法,对不同频率的各次谐波而言,感抗与容抗是不同的,即对k 次谐波有
![]()
【例6-2】 如图6-3(a)所示电路中的电压源为例6-1 中图6-2 所示的电压源。已知:R=5 Ω,L=2 H,计算电感两端的电压u。
解:非正弦周期电流电路的计算步骤如下。
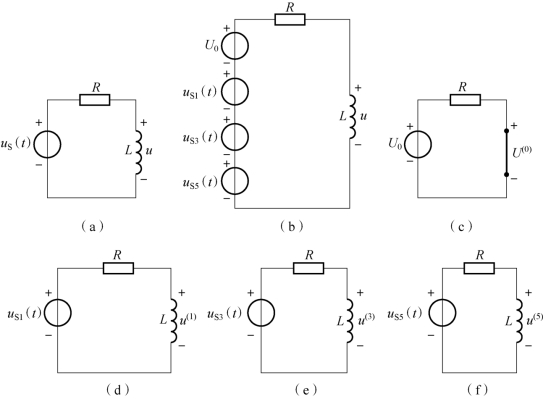
图6-3 例6-2 电路
①由例6-1 可知方波信号的傅里叶级数展开式为
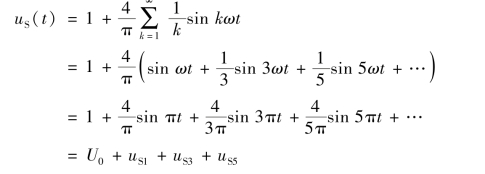
其中,直流分量为
![]()
基波为
![]()
三次谐波为
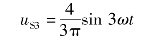
五次谐波为
![]()
因此,图6-3(a)电路可以等效为图6-3(b)电路。(https://www.daowen.com)
②利用叠加定理计算分量。
当直流分量U0单独作用时,电感相当于短路,等效电路如图6-3(c)所示,即
![]()
当基波uS1单独作用时,电路如图6-3(d)所示,对应的感抗为
![]()
根据分压公式,可得
![]()
对应的时域形式为
![]()
当三次谐波uS3单独作用时,电路如图6-3(e)所示,对应的感抗为
![]()
根据分压公式可得
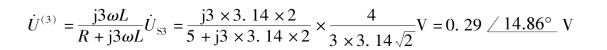
对应的时域形式为
![]()
当五次谐波uS5单独作用时,电路如图6-3(f)所示,对应的感抗为
![]()
根据分压公式可得
![]()
对应的时域形式为
![]()
③把直流分量和各次谐波分量计算结果的瞬时值叠加,即
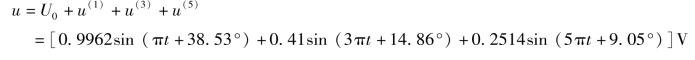
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





