在电子技术、自动控制、计算机和无线电技术等方面，电压和电流是周期性的非正弦波形，如半波整流电路的输出信号、周期性锯齿波信号和方波信号，如图6-1 所示。

图6-1　非正弦周期信号

（a）半波整流电路的输出信号；（b）周期性锯齿波信号；（c）方波信号

非正弦周期信号的特点：不是正弦波同时又按照周期规律变化，满足条件为

式（6-1）中T 为非正弦周期函数f（t）的周期。

已知f（t）为非正弦周期函数，周期为T，角频率为ω。根据傅里叶级数展开式，把非正弦周期函数f（t）展开，即

在式（6-2）中，A0为直流分量，A1mcos（ωt＋φ1）是正弦函数，频率和原函数f（t）的频率相同，称为基波。A2mcos（2ωt＋φ2）是正弦函数，频率为原函数f（t）频率ω的2 倍，称为二次谐波。A3mcos（3ωt＋φ3）是正弦函数，频率为原函数f（t）频率ω的3 倍，称为三次谐波。以此类推，Anmcos（nωt＋φn）称为高次谐波。

由此可以看出，非正弦周期函数可以分解为直流量和多个正弦量的叠加。高次谐波电流会造成电网的电压失真，干扰通信和信号电路。

式（6-2）中的a0、ak、bk为傅里叶系数，计算公式为

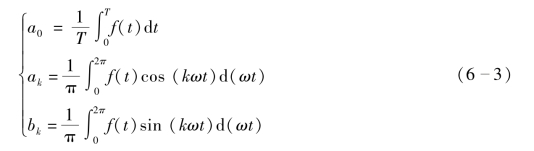
各系数之间的关系为

由以上分析可知，只要求出傅里叶系数a0、ak、bk，就可以写出非正弦周期函数的傅里叶级数展开式。在大多数的电工电子电路中，如果遇到非正弦周期函数，可以直接通过查表得到傅里叶级数展开式。

【例6-1】　把图6-2 所示的方波电压信号uS（t）展开成傅里叶级数。

(www.daowen.com)

图6-2　方波电压信号

解：图6-2 电路所示为周期性方波电压信号，周期T＝2，。uS（t）在一个周期内的函数表示式为

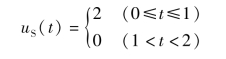
直流分量为

谐波分量为

因此，方波电压信号uS（t）的傅里叶级数展开式为

周期性方波信号可以看成是直流分量与一次谐波、三次谐波、五次谐波等奇次谐波的叠加。

当非正弦周期信号展开成傅里叶级数时，理论上直流量和无穷多次谐波的叠加才能完全逼近原函数。从傅里叶级数展开式可知，随着谐波次数的增高，对应谐波分量的幅值也越来越小，呈收敛性。因此在工程应用过程中，一般只计算前几项。

常见的非正弦周期信号及其对应的傅里叶级数展开式如表6-1 所示。

表6-1　常见的非正弦周期信号及其傅里叶展开式

续表