【摘要】:结合线性无源一端口网络端口电压和端口电流的有效值相量式、有功功率、无功功率、视在功率各自的定义和相互关系,复功率的等式变换推导为注意:①复功率的定义适用于正弦稳态电路中的任何线性的有源或无源的一端口网络和电路中单个的电路元件。
4.6.1 和4.6.2 节明确了正弦稳态电路无源一端口网络所对应的有功功率P、无功功率Q、视在功率S、功率因数角φ的定义和工程意义。为了方便地计算这些参数,引入了正弦稳态电路无源一端口网络复功率的概念。
对应图4-17 所示的正弦稳态电路线性无源一端口网络,端口电压和端口电流的有效值相量式设定为
![]()
则此线性无源一端口网络对应的复功率S 定义式为
![]()
式(4-86)中,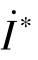 是
是 的共轭复数。
的共轭复数。
复功率的单位为伏安(V·A),与视在功率S的单位相同。
结合线性无源一端口网络端口电压和端口电流的有效值相量式、有功功率、无功功率、视在功率各自的定义和相互关系,复功率的等式变换推导为
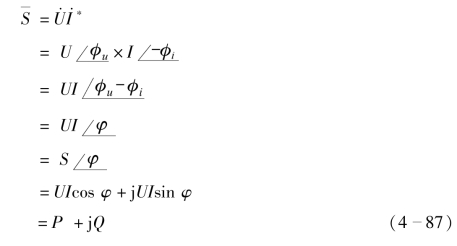
注意:
①复功率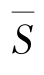 的定义适用于正弦稳态电路中的任何线性的有源或无源的一端口网络和电路中单个的电路元件。
的定义适用于正弦稳态电路中的任何线性的有源或无源的一端口网络和电路中单个的电路元件。
②对于无源的一端口网络,其外电路可以以阻抗Z 或导纳Y 来等效替代,所以复功率S 对应的表达式为(https://www.daowen.com)
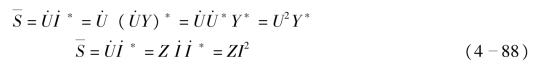
③对于整个正弦稳态电路,所有支路吸收的复功率代数和为0,此为复功率守恒定理。具体对应多种表达形式,即
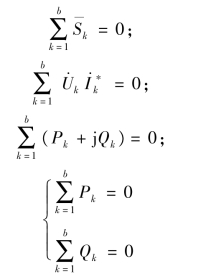
④在具体列式求解复功率时,若对应的电压相量与电流相量呈关联参考方向,则复功率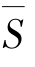 加下标“吸收”,反之,加下标“发出”,且实际吸收的复功率总和等于实际发出的复功率总和。
加下标“吸收”,反之,加下标“发出”,且实际吸收的复功率总和等于实际发出的复功率总和。
【例4-12】 如图4-41 所示的正弦稳态电路相量模型,已知:![]()
![]() ,求该电路各个支路的复功率。
,求该电路各个支路的复功率。
解:求解电路中并联支路的端电压相量,即
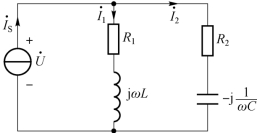
图4-41 例4-12 正弦稳态电路相量模型
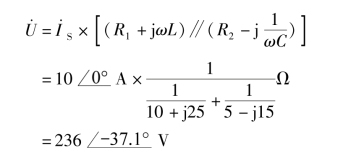
分别求解电流_源支路、电阻串联电感支路、电阻串联电容支路的复功率,即
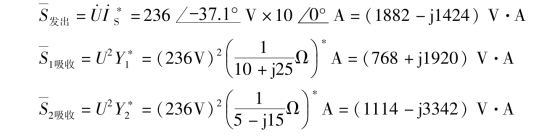
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







