根据有功功率和无功功率的定义，分别求解纯电阻、纯电感、纯电容支路的有功功率和无功功率。

1.电阻元件的有功功率和无功功率

根据式4-21，电阻元件的电压相量与电流相量相位相同，两者的相位差为0°，所以电阻元件的有功功率PR为

电阻元件的无功功率QR为

由式（4-75）和式（4-76）可知，纯电阻元件只吸收（消耗）功率，不能发出功率，不存在能量往复交换的情况。

2.电感元件的有功功率和无功功率

根据式（4-30）知，电感元件的电压相量比电流相量相位超前90°，两者的相位差为90°，所以电感元件的有功功率PL为

电感元件的无功功率QL为

由式（4-77）和式（4-78）可知，纯电感元件的有功功率为0，不消耗功率，存在能量的往复交换的情况。

3.电容元件的有功功率和无功功率

根据式4-43，电容元件的电压相量比电流相量相位滞后90°，两者的相位差为－90°，所以电容元件的有功功率PC为(www.daowen.com)

电容元件的无功功率QC为

由式（4-79）和式（4-80）可知，纯电容元件有功功率也为0，不消耗功率，存在能量的往复交换的情况。

注意：

①在同一个正弦稳态电路中，电感元件的无功功率与电容元件的无功功率在一定程度上具有互相补偿特性：当电感L 发出功率时，电容C 正好吸收功率。正弦稳态电路中电感元件与电容元件对应的瞬时功率波形如图4-36 所示。

在实际工程应用中，经常利用正弦稳态电路中电感元件与电容元件无功功率的互相补偿特性，来提升电路中的功率因数值，进而提高对电能的利用率。

②根据有功功率P、无功功率Q、视在功率S的定义式，可推导出三种类型功率的数值关系式，即

上述关系式可以由功率三角形表示，如图4-37 所示。

图4-36　正弦稳态电路中电感、电容元件瞬时功率波形

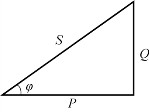
图4-37　正弦稳态电路功率三角形