线性无源一端口网络的阻抗支路如图4-18 所示。线性无源一端口网络在正弦量激励作用下，对外部电路的电路特性可以用等效参数——复阻抗Z（简称阻抗）来表示。

阻抗Z的定义：线性无源一端口网络的端口电压相量与电流相量的比值。定义式为

阻抗Z 是一个复数，因此也被称为复阻抗。阻抗的单位为欧姆（Ω）。

阻抗模为

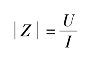
阻抗辐角为

阻抗的辐角实际是正弦稳态电路中对应支路电压与支路电流的相位差。

根据式（4-52）可知，阻抗Z的代数形式为

在式（4-53）中，R 为线性无源一端口网络的等效电阻分量，X 为其等效电抗分量，包括感抗XL和容抗XC。当X>0 时，Z 被称为感性阻抗；当X< 0 时，Z 被称为容性阻抗。

与阻抗Z 相关的几个特征参数可以用阻抗三角形来集中表示参量之间的相互函数关系，如图4-19 所示。

图4-18　线性无源一端口网络的阻抗支路

图4-19　阻抗三角形

用阻抗Z 表达的欧姆定律相量式为

(www.daowen.com)

当正弦稳态交流电路运用相量法进行分析计算时，电路中多个阻抗的串联，等效阻抗等于各个分阻抗的和。

【例4-5】　如图4-20 所示的电路相量图，已知线性无源一端口网络由阻抗Z1、Z2串联构成，求电路对外的总等效阻抗Z。

图4-20　阻抗串联电路

解：根据KVL 相量式，由图4-20 可得

根据阻抗Z 表达的欧姆定律相量式U·＝ZI·，则

根据阻抗的定义，则

阻抗Z1上对应的电压相量为

可得出以下结论：

①串联阻抗电路的总等效阻抗求解式为

②各个分阻抗上分的电压相量与总的端电压相量之间的关系式为

式（4-56）即为串联阻抗电路对应的分压公式。