电阻、电容、电感3 种电路元件是电路中最基本的组成单元。下面分别分析推导3 种线性电路元件的VCR 在正弦稳态交流电路中对应的相量形式。

1.线性电阻元件VCR的相量形式

图4-7　线性电阻支路的时域电路

线性电阻支路的时域电路图如图4-7 所示。已知支路电流的时域形式为

根据线性电阻元件VCR的时域形式，得

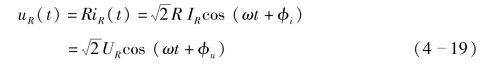
由式（4-19）可以得到线性电阻支路电压与支路电流有效值和初相之间的对应关系式。

有效值关系式为

初相关系式为

根据式（4-18），可以得到线性电阻支路电流的有效值相量式为

根据式（4-19）可以得到线性电阻支路电压的有效值相量式为

根据式（4-20），式（4-21），式（4-23）可以等效变换为

根据式（4-22），式（4-24）可以等效变换为

式（4-25），为线性电阻支路电压与支路电流VCR的相量形式。

式（4-25）也可以表达为

线性电阻支路的相量模型如图4-8 所示，电压和电流对应的相量如图4-9 所示。

图4-8　线性电阻支路的相量模型

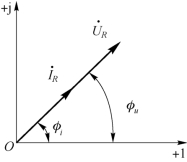
图4-9　线性电阻支路的电压和电流相量

2.线性电感元件VCR的相量形式

线性电感支路的时域电路如图4-10 所示。

已知支路电流的时域形式为

图4-10　线性电感支路的时域电路

线性电感元件VCR的时域形式为

则

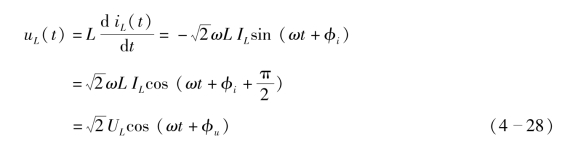
由式（4-28）可以得到线性电感支路电压与支路电流有效值和初相之间的对应关系式。

有效值关系式为

初相关系式

在式（4-29）中，ωL 称为感抗，用XL表示，单位为欧姆（Ω）。由式（4-29）可得

感抗为角频率ω的函数，当电路激励为直流，即ω＝0 时，XL＝ωL＝0，UL＝0，此时电感元件相当于短路；当电路激励为交流，电压值为有限值，且ω→∞时，XL＝ωL→∞，IL＝0，此时电感元件相当于开路。

根据式（4-27），可知线性电感支路电流的有效值相量式为

根据式（4-28）可知线性电感支路电压的有效值相量式为

根据式（4-29）、式（4-30）、式（4-33）可以等效变换为式（4-34），即

根据式（4-32）和式（4-34）可以等效变换为式（4-35），即

式（4-35）为线性电感支路电压与支路电流VCR的相量形式，也可以表达为

根据虚数单位的复数运算式，即

式（4-36）可等效变换为式（4-38），即

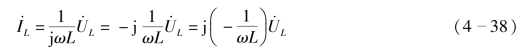(www.daowen.com)

式（4-38）中，称为感纳，用BL表征，单位为西门子（S）。所以式（4-38）也可以表示为

线性电感支路的相量模型如图4-11 所示。电压与电流对应的相量如图4-12 所示。

图4-11　线性电感支路的相量模型

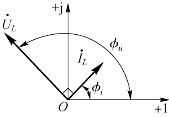
图4-12　线性电感支路电压与电流对应的相量

3.线性电容元件VCR的相量形式

线性电容支路的时域电路如图4-13 所示。

已知支路电压的时域形式为

图4-13　线性电容支路的时域电路

线性电容元件VCR的时域形式为

则

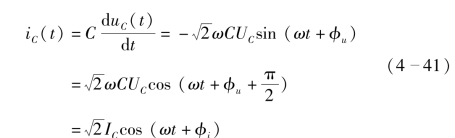
由式（4-41）可以得到线性电容支路电压与支路电流有效值和初相之间的对应关系式。

有效值关系式为

初相关系式为

式（4-42）中，ωC 称为容纳，用BC表示，单位为西门子（S）。由式（4-42）可得

容纳是角频率ω的函数，当电路激励为直流，即ω＝0 时，BC＝ωC＝0，IC＝0，电容元件相当于开路；当电路激励为交流，电流值为有限值，且ω→∞时，BC＝ωC→∞，UC＝0，电容元件相当于短路。

根据式（4-40）得到线性电容支路电压的有效值相量式为

根据式（4-41）得到线性电容支路电流的有效值相量式为

根据式（4-42）、式（4-43）、式（4-46），电流的有效值相量式可以等效变换为

根据式（4-45），式（4-47）可以等效变换为

式（4-48）为线性电容支路电流与支路电压VCR的相量形式，也可以表达为

根据式（4-37）和式（4-49）可以等效变换为（4-50），即

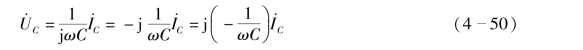
式（4-50）中，称为容抗，用XC表示，单位为欧姆（Ω）。因此，式（4-50）也可以表达为

线性电容支路的相量模型如图4-14 所示，电压与电流对应的相量如图4-15 所示。

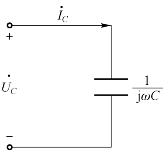
图4-14　线性电容支路的相量模型

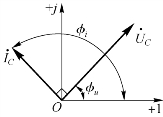
图4-15　线性电容支路电压与电流的相量

注意：

在正弦稳态交流电路中，电阻、电感和电容3 个基本的电路元件各自对应的支路电压与支路电流频率相同，但在相位上存在特定的关系：电阻的支路电压与电流同相位，相位差为0°；电感的支路电压比电流超前90°；电容的支路电压比电流滞后90°。

【例4-4】　已知电阻、电感和电容3 个元件串联构成的正弦稳态交流的电路时域如图4-16（a）所示，已知IS＝5 A，φi＝0°，ω＝103rad/s，R＝3 Ω，L＝1 H，C＝1 μF。求解电流源的端电压u。

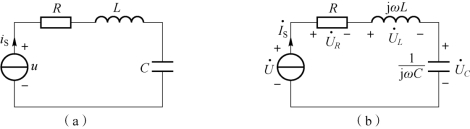
图4-16　例4-7 电路

（a）时域电路；（b）相量模型

解：根据时域电路画出电路对应的相量模型，如图4-16（b）所示。相量模型图中的所有正弦电压量、正弦电流量均以相量标注。电阻、电感、电容元件的标注是以电流相量表征电压相量的VCR 关系式中电流相量之前的阻抗，分别为。

由已知条件IS＝5 A，φi＝0°，列写电流源的电流有效值相量式为

KVL的相量式为

可得

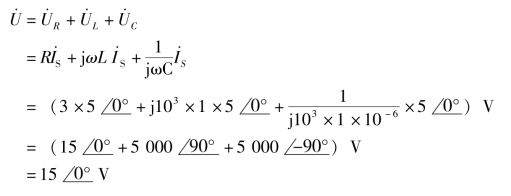
所以

注意：

如果题目已知条件中没有明确电路正弦激励的初相位的值，可以设定串联支路的正弦电流或并联支路的正弦电压初相角为0°，以初相为0°的正弦量的相量作为参考相量，作为后续各个相量参数的计算基础。