1.复数的表示形式
复数有4 种常见的表现形式,分别为代数形式、三角函数形式、指数形式和极坐标形式。
1)复数的代数形式
复数的代数形式为
![]()
式(4-10)中,a 是复数F的实部,b 是复数F的虚部,可分别记为
![]()
式(4-10)中j 为虚数单位,即
![]()
2)复数的三角函数形式
复数对应的复平面坐标如图4-5 所示。
由此得到复数的三角函数形式为

图4-5 复平面坐标
![]()
在式(4-12)中有
![]()
3)复数的指数形式
利用欧拉公式,即
![]()
变换得到复数的指数表现形式,即
![]()
4)复数极坐标形式
由复数的三角函数形式或指数形式可直接列写出对应的极坐标形式,即
![]()
复数之间的加、减、乘、除运算,通过选择合适的复数表现形式,可以使运算简化。
2.复数的运算法则(https://www.daowen.com)
1)复数的加减运算
复数的加、减运算优先选择复数的代数形式,可以实现运算的最简化处理。运算法则:复数相加减,实部与实部相加减,虚部与虚部相加减。其具体形式为
![]()
则
![]()
复数的加、减运算也可以通过在复平面上分别按平行四边形法则和三角形法则进行作图求解,如图4-6 所示。
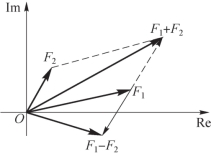
图4-6 复数加、减运算平行四边形作图法
2)复数的乘、除运算
复数的乘、除运算优先选择复数的极坐标形式,运算简单。运算法则:模相乘除,辐角相加减。其具体形式为
![]()
则

复数的乘、除运算有时选择指数形式运算也比较方便。其具体形式为
![]()
则

如果复数最初给定的表现形式不是上述运算所要求的对应形式,则要根据运算需要进行对应表现形式的等效变换。
【例4-1】 已知![]() ,求F1+F2。
,求F1+F2。
解:![]()

注意:
①F·ejθ相当于复数F 沿逆时针方向旋转一个角度θ 而模不变,所以ejθ被称为旋转因子。特殊辐角的旋转因子在复数运算中应用广泛,其极坐标形式与代数形式为
![]()
②若复数![]()
![]() ,则此复数的共轭复数记为F∗
,则此复数的共轭复数记为F∗
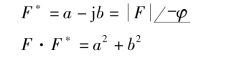
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






