根据电源等效变换,既然独立电压源与电阻的串联可以和独立电流源与电阻的并联进行等效变换,那么含源二端网络也可以等效为独立电流源与电阻的并联,也称为诺顿定理。诺顿定理是由美国工程师诺顿(E.L.Norton)于1926 提出的,其内容如下:任何一个含源线性二端网络,对外电路来说,可以等效为一个独立电流源和电阻(电导)的并联,如图3-14 所示。
图3-14(a)中,独立电流源的电流等于该二端网络的短路电流,参考方向如图3-14(b)所示。而电阻(电导)等于把该二端网络的全部独立电源置零后的输入电阻(电导)。
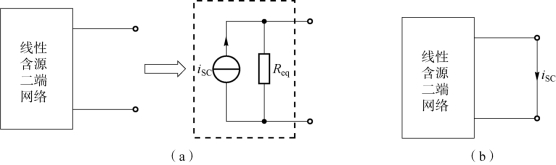
图3-14 诺顿等效电路及电流源电流求解
诺顿等效电路中的等效电阻的求法与戴维南定理中等效电阻的求法相同。
诺顿等效电路中独立电流源的参考方向与线性含源二端网络短路电流参考方向的关系和戴维南定理应用于分析电路时情况相似。
(1)已知一线性二端网络,求解其诺顿等效电路,如图3-15 所示。
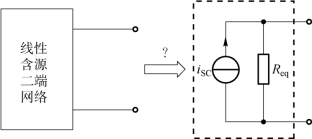
图3-15 线性含源二端网络诺顿等效电路
该题型的解题步骤:利用电源等效变换(有时候是多次利用)把线性含源二端网络化简为一个独立电流源与一个电阻的并联;或者求其短路电流和等效电阻,并画出诺顿等效电路。
(2)在复杂电路中,求解某一支路电压或电流,如图3-16 所示。

图3-16 戴维南定理在带有负载电路中的应用
该题型的解题步骤:断开待求支路(把待求支路从原电路图中移走),标出余下部分的端口;计算余下二端网络的短路电流和诺顿等效电阻,并画出诺顿等效电路;把断开的待求支路连接在诺顿等效电路的两个端子之间,在等效电路中求解参数。
注意:
①当线性含源二端网络的等效电阻Req=0 时,该网络只有戴维南等效电路,而无诺顿等效电路。
②当线性含源二端网络的等效电阻Req=∞时,该网络只有诺顿等效电路,而无戴维南等效电路。
【例3-8】 求解图3-17(a)所示电路的诺顿等效电路。
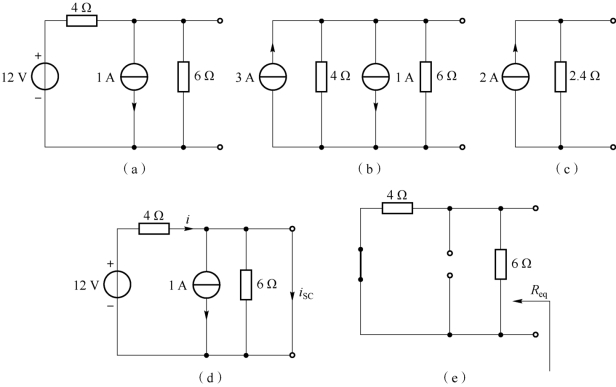
图3-17 例3-8 电路
解:本例题采用两种方法求解。
方法一:电源等效变换法
首先根据电源等效变换,把3-17(a)电路中的12 V 独立电压源与4 Ω 电阻的串联等效为3 A 独立电流源与4 Ω 电阻的并联,如图3-17(b)所示;再把3 A 独立电流源与1 A独立电流源并联(注意参考方向)等效为一个2 A的独立电流源,4 Ω 电阻与6 Ω 电阻并联等效为2.4 Ω 电阻。诺顿等效电路如图3-17(c)所示。
方法二:诺顿定理
①求解短路电流iSC。
首先把线性含源二端网络端口短路,6 Ω 电阻被短路,标出短路电流iSC,设12 V 独立电压源与4 Ω 电阻的串联支路电流为i,参考方向如图3-17(d)所示。列写KCL 方程,即
![]()
列写最大回路的KVL 方程,即(https://www.daowen.com)
![]()
联立以上2 个方程,求解可得
![]()
②求等效电阻Req。
把图3-17(a)电路中的独立电源置0,即12 V 独立电压源短路,1 A 独立电流源开路,如图3-17(e)所示。其等效电阻为
![]()
③画出诺顿等效电路,如图3-17(b)所示。
【例3-9】 利用诺顿定理求解图3-18(a)所示电路的电压u。

图3-18 例3-9 电路
解:求解电压u的步骤如下。
①把待求支路断开,即把5 Ω 所在支路断开,如图3-18(b)所示。
②求解短路电流iSC。把端口短路,标出短路电流iSC,设6 Ω 所在支路电流为i,如图3-18(c)所示。
列写KCL 方程,即
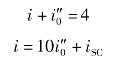
列写回路KVL 方程
![]()
联立以上3 个方程,解得
![]()
③求解等效电阻Req。本例题采用外加电源法计算等效电阻。把图3-18(b)中的独立电源置0,即把4 A 独立电源开路,外加独立电压源uS,独立电压源产生的电流为i1,如图3-18(d)所示。列写KCL 方程,即
![]()
列写最大回路的KVL 方程,即
![]()
联立以上2 个方程可得
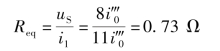
④画出诺顿等效电路,接入5 Ω 所在支路,如图3-18(e)所示,电路的电压为
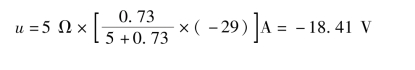
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





