网孔电流法的基本思想：假设每个网孔中都有一个网孔电流沿着构成该网孔的各支路流动，则各支路电流可以用网孔电流的线性组合表示。

在如图2-7 所示电路中，有Ⅰ、Ⅱ、Ⅲ3 个网孔，假设有3 个网孔电流il1、il2和il3沿顺时针方向在流动，可以清楚地看出，当某个支路只属于一个网孔时，那么该支路电流就等于该网孔电流；如果某个支路属于两个网孔所共有，则该支路电流就等于流经该支路的两个网孔电流的代数和。当网孔电流方向与支路电流方向一致时为正，反之为负。

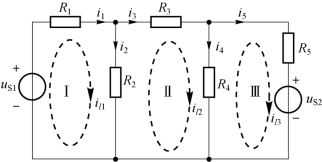
图2-7　网孔电流示例

由于R1和uS1为串联支路，只属于网孔Ⅰ，而且网孔电流il1流过该支路的方向与该支路电流方向一致，所以R1和uS1串联支路电流i1＝il1；电阻R3所在支路只属于网孔Ⅱ，而且网孔电流il2流过该支路的方向与该支路电流方向一致，所以R3所在支路电流i3＝il2；R5和uS2串联支路只属于网孔Ⅲ，而且网孔电流il3流过该支路的方向与该支路电流i5方向一致，所以R5和uS2串联支路电流i5＝il3。

电阻R2所在支路既属于网孔Ⅰ又属于网孔Ⅱ，即网孔电流il1和网孔电流il2都通过电阻R2，因此R2所在支路电流i2为网孔电流il1和网孔电流il2的叠加，同时由于网孔电流il1和支路电流i2参考方向一致，因此il1取正，网孔电流il2和支路电流i2参考方向相反，因此il2取负，即i2＝il1－il2。电阻R4所在支路既属于网孔Ⅱ又属于网孔Ⅲ，即网孔电流il2和网孔电流il3都通过电阻R4，因此R4所在支路电流i4为网孔电流il2和网孔电流il3的叠加，同时由于网孔电流il2和支路电流i4参考方向一致，因此il2取正，网孔电流il3和支路电流i4参考方向相反，因此il3取负，即i4＝il2－il3。

由以上分析可知，只要求得网孔电流，电路中所有的支路电流便可以根据网孔电流与支路电流之间的关系得到。

由图2-7 可知，网孔电流沿着闭合的网孔边界流动，当流过某一个结点时，必然从该结点流入，又从该结点流出，因此网孔电流满足KCL 方程，而且相互独立。网孔电流法是对基本回路列写KVL 方程，方程数为[b－（n－1）]，与支路电流法相比，方程个数减少了（n－1）个。　

网孔电流法分析电路的关键是如何简便、正确地列写出以网孔电流为变量的网孔电压方程。列写网孔电流方程有两种方法：一是直接根据定义列写各网孔的KVL 方程，电阻两端的电压用电阻阻值与该电阻上通过的所有网孔电流的代数和表示，此方法称为一般方法；二是观察法。下面分别进行介绍。

方法一：

利用一般方法列写网孔电流方程的步骤如下：

①找到网孔，在网孔中标出网孔电流及其参考方向；

②以网孔电流为未知量列写每个网孔的KVL 方程，绕行方向取该网孔的网孔电流方向。列写KVL 方程时，电阻两端的电压用电阻阻值与该电阻上通过所有网孔电流代数和的乘积表示，当流过某个电阻的网孔电流与绕行方向一致时取正，反之取负。

下面以图2-7 电路为例，分别列写网孔的KVL 方程。

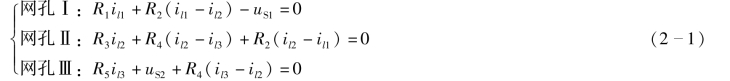
整理后可得

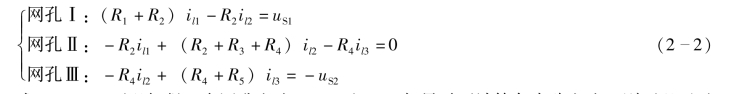
式（2-2）可以解得3 个网孔电流il1、il2和il3。如果需要计算各支路电流，则可以通过支路电流与网孔电流的关系得

【例2-6】　已知图2－8（a）所示电路中，R1＝R3＝R4＝1 Ω，R2＝2 Ω，uS1＝3 V，uS2＝1 V，利用网孔电流法计算R2两端的电压u。

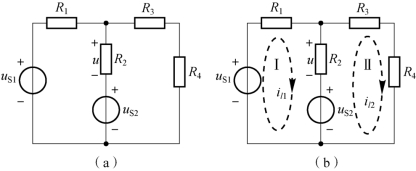
图2-8　例2-6 电路

解：图2-8（a）所示电路中有两个网孔，在两个网孔中标出网孔电流il1和il2，参考方向取顺时针，如图2-8（b）所示。对两个网孔列写KVL 方程，回路绕行方向取该回路网孔电流的参考方向，电阻上的电压用电阻阻值与通过该电阻所有网孔电流代数和的乘积表示。

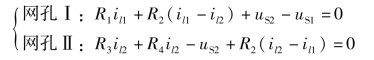
把已知条件代入，整理可得

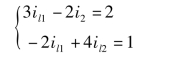
解得

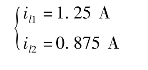
电压u 为电阻R2两端的电压，R2上共有两个网孔电流il1和il2流过，且网孔电流il1的参考方向与电压u 参考方向相关联，网孔电流il2的参考方向与电压u 参考方向非关联，因此

以上是列写网孔电流方程的一般方法，此方法在应用时虽然简单，但容易漏掉电阻上流过的网孔电流。

方法二：

式（2-2）为利用一般方法对图2-7 列出的网孔电流方程，对图2-7 分别列写网孔的KVL 方程。

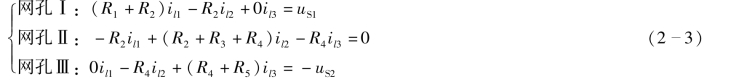
由式（2-3）可知，在网孔Ⅰ的网孔电流方程中，il1前的系数（R1＋R2）是网孔Ⅰ中所有的电阻和，用R11表示，因此，R11称为网孔Ⅰ的自电阻；il2前的系数（－R2）是网孔Ⅰ和网孔Ⅱ公共支路上的电阻，用R12表示，R12称为网孔Ⅰ和网孔Ⅱ的互电阻，由于流过R2的网孔电流il1和il2方向相反，因此R2前为负号；il3前的系数为0，是网孔Ⅰ和网孔Ⅲ公共支路上的电阻，用R13表示，R13称为网孔Ⅰ和网孔Ⅲ的互电阻，由于网孔Ⅰ和网孔Ⅲ之间没有公共电阻，因此网孔Ⅰ和网孔Ⅲ的互电阻R13＝0 ；等式的右边uS1表示网孔Ⅰ中所有电压源的代数和，用uS11表示，即网孔Ⅰ中的等效电压源，若电压源电压的方向与网孔电流方向相反，则取正号，否则为负，即等号的右边为网孔Ⅰ所有等效电压源的电压升的代数和，沿着该网孔电流方向进行绕行，当经过等效电压源时，如果电压方向为从负流向正，则取正号，反之取负号。

同理可以得出网孔Ⅱ的网孔电流方程中的自电阻、互电阻和等效电压源分别如下。

自电阻：R22＝R2＋R3＋R4

互电阻：R21＝－R2，R23＝－R4

等效电压源：uS22＝0

网孔Ⅲ的网孔电流方程中的自电阻、互电阻和等效电压源分别如下。

自电阻：R33＝R4＋R5

互电阻：R31＝0，R32＝－R4

等效电压源：uS33＝－uS2

因此，可以得到3 个网孔的网孔电流方程的标准形式为

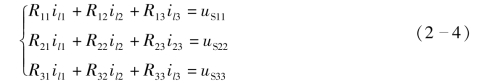
对于具有l＝b－（n－1）个基本（独立）回路的电路，网孔电流方程的标准形式为(www.daowen.com)

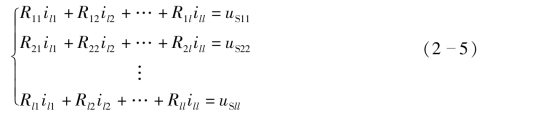
其中，自电阻Rkk为网孔k 中所有的电阻和，自电阻始终为正；互电阻Rjk和Rkj为网孔k 和网孔j的公共电阻和，可以是正数或负数，也可以为0，当流过互电阻的两个网孔电流方向相同时，互电阻为正，当流过互电阻的网孔电流方向相反时，互电阻为负，如果两个网孔没有公共电阻，则互电阻为0。等效电压源uSkk为网孔k 中所有等效电压源的电压升的代数和，沿着该网孔电流方向进行绕行，当经过等效电压源时，如果电压方向为从负流向正，则其符号为正，反之为负。

网孔电流方程的实质是对网孔列写KVL 方程。因此，方程等号的左边是各网孔电流在任一网孔中电阻电压的代数和；方程等号的右边是在无电流源的情况下，该网孔中各电压源产生的电压的代数和。当电路中不含受控源时，网孔电流方程的系数矩阵为对称阵。

从以上分析可以看出，由独立电压源和线性电阻构成电路的网孔电流方程，其系数很有规律，可以用观察电路图的方法直接写出网孔电流方程。

通过观察得到自电阻、互电阻和等效电压源，代入网孔电流方程的标准形式，这种方法称为观察法，也称为标准形式法或格式化方法。

观察法列写网孔电流方程的解题步骤如下：

（1）找到网孔，标出各网孔电流及其参考方向；

（2）写出网孔电流方程的标准形式，通过观察，计算出自电阻、互电阻和网孔中电压源电压的代数和，代入网孔电流方程的标准形式；

（3）求解网孔电流方程，得到网孔电流方程；

（4）进行其他分析。

【例2-7】　在如图2-9（a）所示电路中，uS1＝20 V，uS2＝10 V，uS3＝5 V，R1＝6 Ω，R2＝4 Ω，R3＝6 Ω，R4＝10 Ω，R5＝2 Ω，R6＝8 Ω，用网孔电流法求各支路电流。

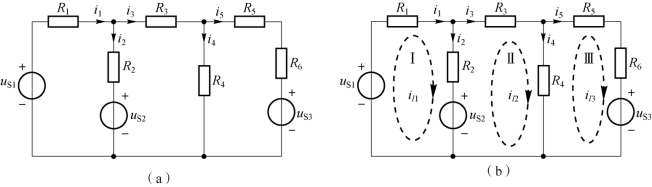
图2-9　例2-7 电路

解：分别用一般方法和观察法列写网孔电流方程。

方法一：一般方法

①找到网孔，标出网孔电流及其参考方向。图2-9（a）中共有3 个网孔，网孔电流分别为il1、il2和il3，参考方向全部取顺时针，如图2-9（b）所示。

②列写3 个网孔的KVL 方程。

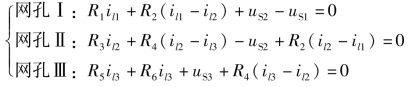
代入数据整理可得网孔电流方程为

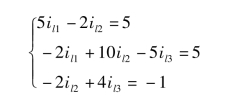
③求解网孔电流方程，可得

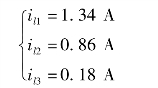
④根据支路电流与网孔电流的关系，可以求得各支路电流为

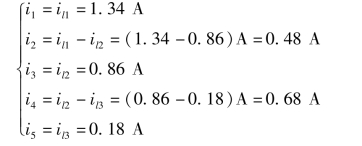
方法二：观察法

①找到网孔，标出网孔电流及其参考方向。图2-9（a）共有3 个网孔，网孔电流分别为il1、il2和il3，参考方向全部取顺时针，如图2-9（b）所示。

②写出网孔电流方程的标准形式，通过观察得到各个网孔的自电阻、互电阻和等效电压源。

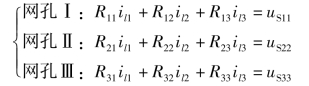
通过观察可得

网孔Ⅰ自电阻：R11＝R1＋R2

网孔Ⅱ自电阻：R22＝R2＋R3＋R4

网孔Ⅲ自电阻：R33＝R4＋R5＋R6

网孔Ⅰ与网孔Ⅱ的互电阻：R12＝R21＝－R2

网孔Ⅱ与网孔Ⅲ的互电阻：R23＝R32＝－R4

网孔Ⅰ与网孔Ⅲ的互电阻：R13＝R31＝0

网孔Ⅰ的等效电压源：uS11＝uS1－uS2

网孔Ⅱ的等效电压源：uS22＝uS2

网孔Ⅲ的等效电压源：uS33＝－uS3

代入标准形式的网孔电流方程中，可得

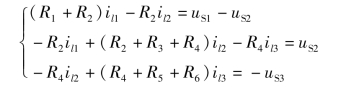
化简为

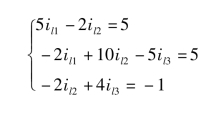
③求解网孔电流方程，可得

④根据支路电流与网孔电流的关系，可以求得各支路电流为