支路电流法适用于含有独立电压源与电阻的电路。当电路中含有独立电流源时，包含两种情况：一是独立电流源与电阻的并联；二是只有独立电流源。

当独立电流源与电阻并联时，首先利用电源的等效变换将其转换为独立电压源与电阻的串联，然后利用支路电流法的解题方法与步骤进行求解。

当电路中只含有独立电流源时，由于独立电流源的端电压是由外电路与其电流共同决定的，在列写KVL 方程时其端电压无法表示，因此需要做特殊处理。方法有如下两种。

方法一：

设独立电流源两端电压，把独立电流源当作电压源来列写方程，由于多了独立电流源电压这一未知数，因此需要增补方程。增补方程的原则是利用已知条件的同时不再增加未知数，因此补充独立电流源的电流与支路电流之间的关系方程，令独立电流源所在支路电流等于独立电流源的电流即可。

方法二：

在选取回路列KVL 方程时，避开独立电流源所在的支路，同时把独立电流源所在支路的电流作为已知条件。

【例2-2】　利用支路电流法计算如图2-3（a）所示电路的电压u。

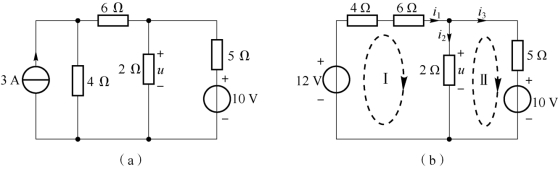
图2-3　例2-2 电路

解：在图2-3（a）所示电路中，包含了3 A 独立电流源与4 Ω 电阻的并联，通过电源等效变换为独立电压源与电阻的串联，独立电压源为3 A×4 Ω＝12 V，串联的电阻为4 Ω，等效电路如图2-3（b）所示。根据支路电流法进行分析。

在图2-3（b）电路中，标示出各个支路的支路电流i1、i2、i3。该电路共有两个结点，任选其中一个结点列写KCL 方程，即

选取两个网孔列写KVL 方程，其回路绕行方向如图2-3（b）所示。

网孔Ⅰ：4i1＋6i1＋2i2－12＝0

网孔Ⅱ：10＋5i3－2i2＝0

联立KCL 方程和KVL 方程，求解可得

【例2-3】　利用支路电流法求解如图2-4（a）所示电路的支路电流。

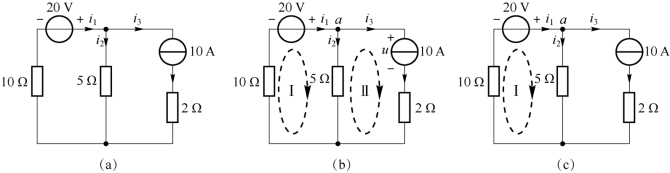
图2-4　例2-3 电路

解：图2-4（a）电路中含有独立电流源，故可以利用如下两种方法进行求解。(www.daowen.com)

方法一：

设电流源两端电压，并将电流源看作电压源。

（1）对结点a 列KCL 方程，即

（2）设电流源两端电压为u，参考方向如图2-4（b）所示，选两个网孔为独立回路，列写KVL 方程。

回路Ⅰ：5i2＋10i1－20＝0

回路Ⅱ：u＋2i3－5i2＝0

（3）由于多出一个未知量u ，因此需要增补一个独立电流源电流与支路电流之间的关系方程，独立电流源所在支路电流等于该独立电流源电流。补充方程为

联立以上方程，求解可得各支路电流为

方法二：

列写KCL 方程，且在列写KVL 方程时避开独立电流源所在的支路。由于独立电流源所在支路的支路电流等于独立电流源电流，因此该支路电流可以作为已知条件，即

两个支路电流未知，因此只需列写两个方程。

（1）对结点a 列写KCL 方程，即

（2）避开独立电流源支路取回路，选左边的网孔，绕行方向如图2-4（c）所示，列写KVL 方程为

联立方程求各支路电流得