对于一个含有n 个结点、b 条支路的电路可以列写（n－1）个独立的KCL 方程，（b－n＋1）个独立的KVL 方程，如果把电阻的VCR 方程（u＝Ri）或支路的VCR 方程代入到KVL 方程中，则KVL 方程就变成了含有支路电流的方程。将KVL 方程与KCL 方程联立，就可以得到以支路电流为变量的b 个独立的方程，这种分析方法称为支路电流法。

支路电流法列写的是KCL 方程和KVL 方程，方程列写方便、直观，但方程数较多，适用于支路数目不多的电路分析。

根据以上分析，可以得到支路电流法的解题方法与步骤如下：

（1）在电路图上标出各支路电流和电压的参考方向；

（2）从电路的n 个结点中任意选择（n－1）个结点列写KCL 方程；

（3）选择（b－n＋1）个回路，指定回路的绕行方向，结合元件的特性（VCR 方程）列写用支路电流表示的KVL 方程；

（4）联立KCL 和KVL 方程，求解上述b 个方程，得到b 条支路的支路电流；

（5）进一步计算支路电压或进行其他分析。

【例2-1】　在如图2-2（a）所示电路中，已知uS1＝12 V，uS2＝20 V，R1＝3 Ω，R2＝2 Ω，R3＝5 Ω，用支路电流法计算各支路电流。(www.daowen.com)

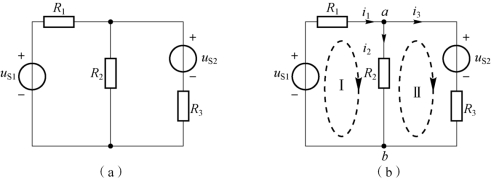
图2-2　例2-1 电路

解：标出各支路电流，符号及参考方向如图2-2（b）所示，参考方向可以任意标示。电路中有2 个结点，因此，可以列写n－1＝2－1＝1 个独立的KCL 方程。

①对结点a 列写KCL 方程，即

②对回路Ⅰ、回路Ⅱ分别列写KVL 方程，绕行方向如图2-2（b）所示，同时把电阻的VCR 方程（u＝Ri）代入KVL 方程。

③联立KCL、KVL 方程求解，得：