对于一个无源（不含独立源）二端网络，无论其内部如何复杂，如果在其端口加上独立电源，则端口电压与端口电流的比值定义为该二端网络的输入电阻，也称为等效电阻。

根据输入电阻的定义，计算输入电阻的方法有以下两种。

（1）如果二端网络的内部仅含电阻，不含受控源，则可以利用电阻的串并联和Y－Δ 等效变换的方法求解等效电阻，输入电阻等于其等效电阻。

（2）如果二端网络内部含有受控源和电阻，则根据输入电阻的定义求解，即利用在二端网络端口加电源的方法求输入电阻：

①在二端网络的端口加电压源，列出其端口电压与端口电流的关系式，然后计算端口电压和端口电流的比值，求得输入电阻。如图1-95（a）所示，输入电阻为

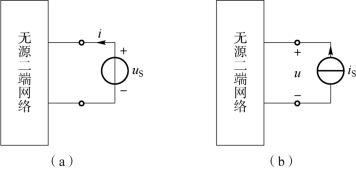
图1-95　外加电源法求解输入电阻

（a）外加电压源；（b）外加电流源

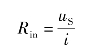
②在二端网络的端口加电流源，列出其端口电压与端口电流的关系式，然后计算端口电压和端口电流的比值，求得输入电阻。如图1-95（b）所示，输入电阻为

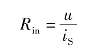
这种方法称为外加电源法，此时，端口电压和端口电流不一定给出确定的数值，只要找出它们的关系即可。

注意：

利用外加电源法时，端口电压、电流的参考方向对二端网络来讲应该是关联的。

【例1-24】　求图1-96 所示两个二端网络的输入电阻Rin。

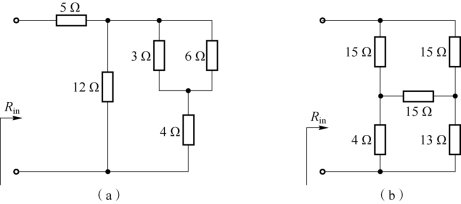
图1-96　例1-24 电路

解：由于图1-96 所示二端网络只含有电阻，因此，等效电阻就是输入电阻，可利用电阻的串并联或Y－△变换等效公式进行计算。

在图1-96（a）电路中，电路的连接方式为3 Ω 电阻与6 Ω 电阻并联，等效电阻为

等效电路如图1-97（a）所示。与4 Ω 电阻串联后，等效电阻为

等效电路如图1-97（b）所示。与12 Ω 电阻并联后，等效电阻为

等效电路如图1-97（c）所示。最后与5 Ω 电阻串联，等效电阻为

等效电路如图1-97（d）所示。

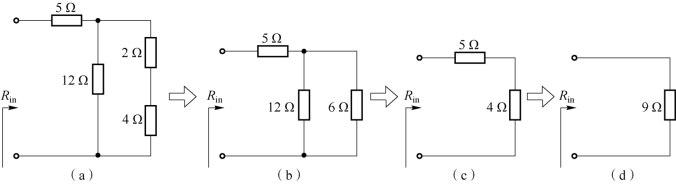
图1-97　例1-24 图1-95（a）解题过程

在图1-96（b）电路中，首先把△连接的3 个15 Ω 电阻等效变换为3 个Y 连接的电阻

如图1-98（a）所示。再利用串并联等效进行计算。电阻的连接方式为5 Ω 电阻与4 Ω电阻串联，等效电阻为(www.daowen.com)

另一条支路的5 Ω 电阻与13 Ω 电阻串联，等效电阻为

等效电路如图1-98（b）所示。然后9 Ω 电阻与18 Ω 电阻并联，再与5 Ω 电阻串联，等效电阻为

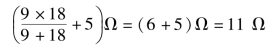
化简电路如图1-98（c）所示。

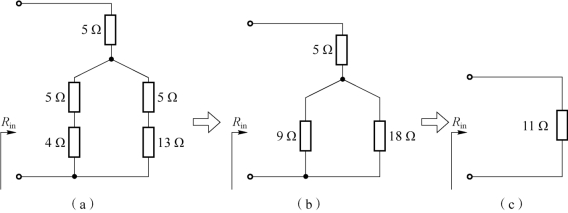
图1-98　例1-24 图1-96（b）解题过程

【例1-25】　求图1-99（a）所示电路的输入电阻Rin。

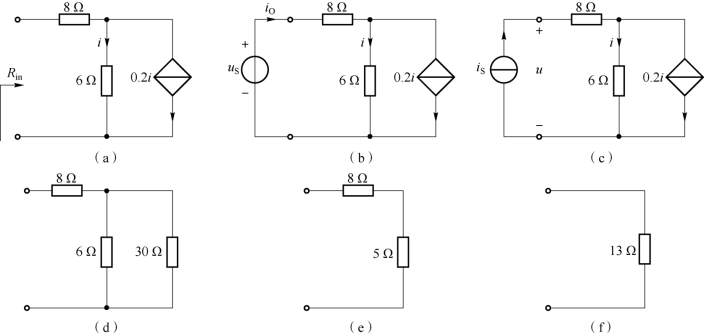
图1-99　例1-25 电路

解：图1-99（a）所示电路中含有受控源，因此采用外加电源法求输入电阻。

方法一：

如图1-99（b）所示，在二端网络的端口外加电压源uS，设在端口产生的电流为iO，列出端口电压与端口电流的表达式。KCL 方程为

对左边网孔列写KVL 方程为

根据输入电阻的定义计算输入电阻为

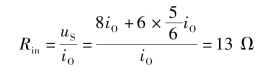
方法二：

如图1-99（c）所示，在二端网络的端口外加电流源iS，端口电压设为u，列出端口电压与端口电流的表达式。KCL 方程为

对左边网孔列KVL 方程为

根据输入电阻的定义计算输入电阻为

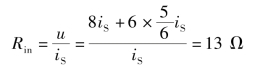
方法三：

如图1-99（a）所示电路中受控电流源与6 Ω 电阻并联，6 Ω 电阻两端的电压为6i，因此，受控电流源的电压也为6i，受控电流源的等效电阻为

如图1-99（d）所示。6 Ω 电阻与30 Ω 电阻并联，等效电阻为

如图1-99（e）所示。5 Ω 电阻与8 Ω 电阻串联，等效电阻为13 Ω，如图1－99（f）所示。