前面已介绍过电阻的串联、并联和串并联，但是在一些电路中，电阻的连接方式并不只有这几种，还有星形（Y）连接和三角形（△）连接。例如，在电力电子系统、传输电网和滤波器等电子设备电路中经常会遇到Y 连接和△连接，如果把△连接等效变换为Y 连接或者把Y 连接等效变换为△连接，电路就可以等效变换为串并联连接电路，简化电路的分析和计算。

1.电阻的Y 连接和△连接

电阻的Y 连接和△连接电路如图1-87 所示（a）所示。为电桥电路，电路中的电阻既不是串联也不是并联，而是Y 连接和△连接，其中R1、R3和R5，R2、R4和R5分别构成了△连接，而R1、R2和R5，R3、R4和R5分别构成了Y 连接。图1－87（b）和图1－87（c）的连接方式为△连接方式，其中图1－87（c）也称为π 形电路。图1－87（d）和图1－87（e）的连接方式为Y 连接方式，其中，图1－87（e）也称T 形电路。因此，电阻的Y 连接和△连接可以这样来定义：如果3 个电阻的一端连在一起，另一端分别与外电路相连，那么就构成Y 连接。如果3 个电阻的首尾相连，形成一个三角形，三角形的3 个顶点分别与外电路相连，那么就构成△连接。电阻的Y 连接和电阻的△连接都属于三端网络。当Y 连接和△连接中的电阻满足一定关系，且它们的端口特性相同时，对外电路而言，能够相互等效变换，即Y 连接可以等效变换为△连接，△连接也可以等效变换为Y 连接。

2.△－Y 电路的相互等效变换

△连接电路等效变换为Y 连接电路，就是在已知△连接电路中的3 个电阻的前提下，首先画出等效Y 连接电路，然后根据变换公式求出Y 连接电路的3 个电阻。而Y 连接电路等效变换为△连接电路，就是在已知Y 连接电路中的3 个电阻的前提下，首先画出等效△连接电路，然后根据变换公式求出△连接电路的3 个电阻。

电阻的△连接和Y 连接电路如图1－88 所示，下面通过两种方法来推导△－Y的变换公式和Y－△的变换公式。

图1-87　电阻的Y 连接和△连接电路

方法一：

利用等效的基本概念，分别写出Y 和△连接电路的端口电流和电压的表达式，令其相等。

图1-88　电阻的△连接和Y 连接电路

（a）△连接；（b）Y 连接

为了便于计算，△连接和Y 连接的3 个端子通常标上序号1、2、3。在Y 连接电路中，与端子1 相连的电阻记作R1，与端子2 相连的电阻记作R2，与端子3 相连的电阻记作R3。在△连接电路中，连接在端子1 和端子2 之间的电阻记作R12，连接在端子2 和端子3 之间的电阻记作R23，连接在端子3 和端子1 之间的电阻记作R31。

△连接的三端网络端子1、2、3 上的电流分别记作i1△、i2△和i3△，端子1、2、端子2、3 以及端子3、1 之间的端口电压分别记作u12△、u23△和u31△，参考方向如图1-88（a）所示。根据KCL 和欧姆定律，在△连接电路中用3 个端口电压u12△、u23△和u31△表示端子的电流i1△、i2△和i3△。的表达式为

Y 连接的三端网络端子1、2、3 上的电流分别记作i1Y、i2Y和i3Y，端子1、2、端子2、3以及端子3、1 之间的端口电压分别计作u12Y、u23Y和u31Y，参考方向如图1-88（b）所示，根据KVL 和欧姆定律，在Y 连接电路中用3 个端子电流i1Y、i2Y和i3Y来表示3 个端口电压u12Y、u23Y和u31Y的表达式为

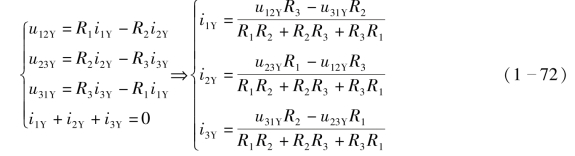
根据等效的条件，对应的端口特性应相同，即

即式（1-71）与式（1-72）的系数相等，此时，可以得到Y→△连接的表达式为

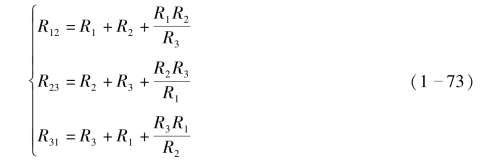
或

同理，可以得到△→Y 连接的表达式为

或

方法二：

△连接电路和Y 连接电路都是三端元件，在求两个端子之间的等效电阻时，把另外一个端子断开。例如，在图1-88（a）所示的△连接电路中，当求端子1 和端子2 之间的电阻R12时，先把端子3 断开，此时，R23和R31串联，再和R12并联，即

在图1-88（b）所示的Y 连接电路中，求R12时，也要把端子3 断开，此时，R1和R2串联，即

根据等效条件u12△＝u12Y，i1△＝i1Y，i2△＝i2Y，可知

即

同理

联立式（1-77）、式（1-78）和式（1-79），可得

和

方法一和方法二得到的结果一样。

电阻△连接等效变换为电阻Y 连接的公式可以简单记忆为

电阻Y 连接等效变换为电阻△连接的公式可以简单记忆为

如果在△连接电路或者Y 连接电路中的3 个电阻相等（对称），即

（1）当R12＝R23＝R31＝R△时，有(www.daowen.com)

（2）当R1＝R2＝R3＝RY时，有

3 个相等电阻的Y 连接和△连接的等效变换如图1-89 所示。等效电阻可以简单记忆为外大里小，外面是△连接，里面是Y 连接，即

图1-89　3 个相等电阻的Y 连接和△连接的等效变换

注意：

①△－Y 电路的等效变换属于多端子电路的等效，在应用中，除了正确使用电阻变换公式计算各电阻值外，还必须正确连接各对应端子；

②等效对外部（端子以外）电路有效，对内部不成立；

③等效电路与外部电路无关；

④等效变换应用于简化电路，不要把本是串并联的问题看作△、Y 结构进行等效变换，那样会使问题的计算更复杂。

（1）在分析和计算电路时，如果需要△→Y的变换，其解题步骤如下：

①在需要变换的△连接电路的3 个端子上分别标上序号1、2、3，标注对应的电阻为R12、R23、R31；

②画等效电路：先画出外电路，然后在端子1、2、3 之间画出3 个电阻的Y 连接，对应的电阻标上R1、R2、R3；

③根据△→Y的相关公式计算等效后的Y 连接对应电阻的阻值。

（2）如果需要Y→△的变换，其解题步骤如下：

①在需要变换的Y 连接电路的3 个端子上分别标上序号1、2、3，标注对应的电阻R1、R2、R3；

②画等效电路：先画出外电路，然后在端子1、2、3 之间画出3 个电阻的△连接电路，对应的电阻标上R12、R23、R31；

③根据Y→△的相关公式计算等效后的△连接对应电阻的阻值。

【例1-21】　求图1-90（a）所示电路的等效电阻Req。

图1-90　例1-21 电路

解：有两种方法可以求解。

方法一：

将10 Ω、10 Ω 和20 Ω 电阻构成的△连接电路等效变换为Y 连接。在其3 个端子上标上序号1、2、3，如图1-90（b）所示，则R12＝10 Ω，R23＝10 Ω，R31＝20 Ω，然后在端子1、2、3 之间画出电阻的Y 连接，与端子1 相连的电阻标上R1，与端子2 相连的电阻标上R2，与端子3 相连的电阻标上R3，如图1-90（c）所示；根据等效变换的公式可得

在图1-89（c）中利用电阻的串联和并联公式，求得等效电阻Req为

方法二：

将20 Ω、10 Ω 和1 Ω 电阻构成的Y 连接电路等效变换为△连接电路，如图1-90（d）所示。在Y 连接的3 个端子上标出1、2、3，即

然后画出等效电路，如图1-90（e）所示。

根据串并联特点及等效，可得

另外也可以把将10 Ω、1.5 Ω 和1 Ω 电阻构成的△连接电路等效变换为Y 连接，或者将10 Ω、10 Ω 和1.5 Ω 电阻构成的Y 连接电路等效变换为△连接电路。读者可以自行分析和计算。

【例1-22】　求图1-91（a）所示电路中的电流i。

图1-91　例1-22 电路

解：首先把需要等效变换的△连接的3 个电阻20 Ω、50 Ω、30 Ω 用圆圈出，对3 个端子进行标号1、2、3，如图1-91（b）所示。则

然后画△→Y 等效电路，即在端子1、2、3 之间画出电阻的Y 连接，与端子1 相连的电阻标上R1，与端子2 相连的电阻标上R2，与端子3 相连的电阻标上R3，如图1-91（c）所示。根据等效变换的公式可得

在图1-91（c）中，根据电阻的串并联，可得出与电压源相连的二端网络的等效电阻为

电路中电流i 为