在实际电路中，理想电压源和理想电流源并不存在，它们只是实际电源的理想模型。蓄电池、干电池、光电池等都属于实际电源。由于实际电源存在着内阻，因此，实际电源的输出电压、电流通常与负载有关系。

1.实际电源的两种模型

实际电源VCR 特性测试电路与特性曲线如图1-78 所示。

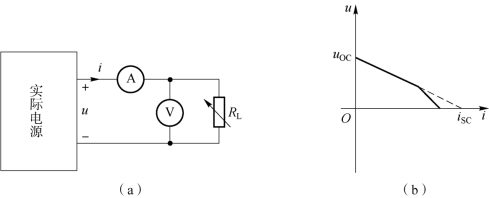
图1-78　实际电源VCR 特性测试电路与特性曲线

（a）VCR 测试电路；（b）特性曲线

由图1-78（b）可知，实际电源的端口电压u 随着端口电流i的增大而减小。当电流超过某一值时，电压会急剧下降，但是为得到实际电源的等效模型，把直线部分进行延长，即图178（b）中的虚线部分，直线与i 轴的交点为实际电源短路时的电流iSC，与u 轴的交点为实际电源的开路电压uOC。因此可以得到实际电源的VCR 方程为

其中，uS为实际电源的开路电压，即RL＝∞时实际电源的端口电压；RS为电源的内电阻，由直线的斜率确定。因此，实际电源模型可以等效为理想电压源和电阻的串联，如图1－79（a）所示。电源的内阻越小，其输出电压越稳定，该模型称为电压源模型。当实际电压源的内阻趋于0 时，即为理想电压源。

根据图1-78（b）所示的特性曲线，列出电源的端口电流和电压之间的表达式为

其中，iS为负载短路时的电流；RS为电源的内电阻，由电流特性的直线斜率决定。因此实际电源模型又可以等效为电流源和电阻的并联，如图1-79（b）所示，并联的电阻越大，电源输出的电流越稳定，该模型称为电流源模型。当实际电流源的内阻趋于∞时，即为理想电流源。

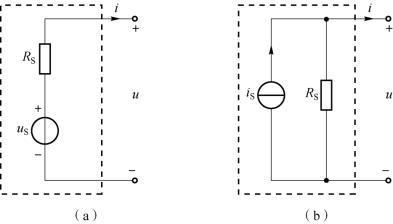
图1-79　实际电源的两种模型

（a）电压源模型；（b）电流源模型

2.实际电源两种模型的等效变换

实际电源有两种模型：电压源模型和电流源模型。这两种模型可以进行等效变换，也称为电源等效变换。等效变换在某些情况下可以使电路的分析变得更为简单。根据等效变换的定义，在等效变换过程中端口的电压、电流应保持不变。

根据KVL 和欧姆定律，实际电压源模型的端口特性（VCR）为

根据KCL 和欧姆定律，实际电流源模型的端口特性（VCR）为

根据等效变换的概念，式（1-69）和式（1-70）对应的系数应该相等，因此，可以得出实际电源两种模型等效变换的条件，即

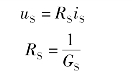
根据以上分析可知，电压源与电阻的串联可以等效为电流源和电阻的并联，如图1－80所示。电流源与电阻的并联可以等效为电压源和电阻的串联，如图1-81 所示。等效的条件就是实际电源两种模型等效变换的条件。

注意：

①电源等效除了数值上要满足等效变换的条件，还要满足方向上的关系：电流源电流方向与电压源电压方向相反，即电流源的电流应从电压源的正极流出；

②这种互换是电路等效变换的一种方法，是对电源以外部分的电路等效，对电源内部电路是不等效的；

③理想电压源与理想电流源的定义本身是相互矛盾的，不会有相同的VCR，因此不能相互转换。

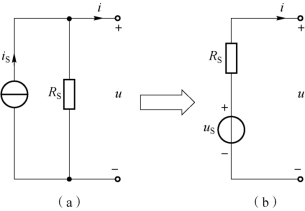
图1-80　电压源与电阻的串联等效为电流源与电阻的并联

（a）电压源与电阻的串联；（b）电流源与电阻的并联

图1-80 中等效变换满足的关系式为

(www.daowen.com)

图1-81　电流源与电阻的并联等效为电压源与电阻的串联

图1-81 中等效变换满足的关系式为

电压源和电阻的串联与电流源和电阻的并联之间的等效变换常常用来化简电路。等效的步骤：首先画出等效电路，在等效电路图中标出电源的参考方向，然后根据数值关系计算等效电路中元件的参数。

【例1-17】　通过电源等效变换求如图1-82 所示电路的等效电路。

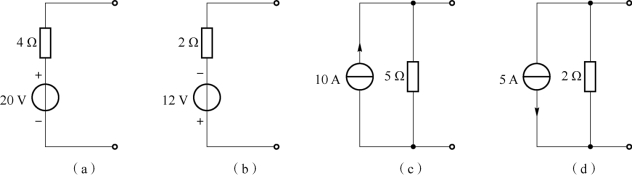
图1-82　例1-17 电路

解：根据电压源和电阻的串联与电流源和电阻的并联之间的等效变换，画出相应的等效电路，标出电源的参考方向，根据数值关系计算元件参数。

图1-82（a）的等效电路如图1-83（a）所示，其中　；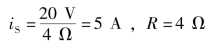

图1-82（b）的等效电路如图1-83（b）所示，其中；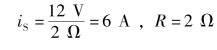

图1-82（c）的等效电路如图1-83（c）所示，其中　uS＝10 A×5 Ω＝50 V ，R＝5 Ω；

图1-82（d）的等效电路如图1-83（d）所示，其中　uS＝5 A×2 Ω＝10 V ，R＝2 Ω。

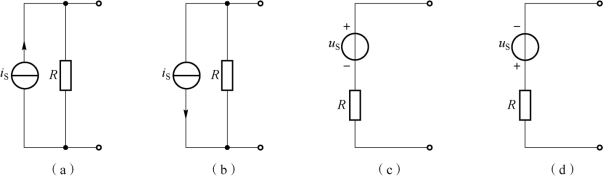
图1-83　例2-17 解题

【例1-18】　求解如图1-84（a）所示电路中的电流i。

图1-84　例1-18 电路

解：根据电源等效变换，首先把3 Ω 电阻与15 V 电压源串联支路等效为电流源与电阻的并联，电流源大小为，并联的电阻为3 Ω；40 V 电压源与20 Ω 电阻串联支路等效为电流源与电阻并联，电流源大小为，并联的电阻为20 Ω；2 A 电流源与2 Ω 电阻并联支路等效为电压源与电阻串联，电压源大小为2 A×2 Ω＝4 V，串联的电阻为2 Ω；等效电路如图1-84（b）所示。

图1-84（b）电路中，3 Ω 电阻与6 Ω 电阻并联等效为2 Ω 电阻，和5 A 电流源并联，根据电源等效变换，可以等效为电压源与电阻串联，电压源为2 Ω×5 A＝10 V，串联的电阻为2 Ω；2 A 电流源与3 A 电流源并联等效为1 A的电流源（注意参考方向），然后和20 Ω电阻并联，根据电源变换等效电压源与电阻串联，电压源为1 A×20 Ω＝20 V，串联的电阻为20 Ω，如图1-84（c）所示。在图1-84（c）回路中列KVL 方程为

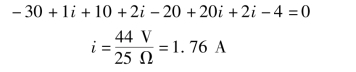
也可以对图1-84（c）进行等效变换，图1-84（c）中30 V 电压源、10 V 电压源、20 V电压源与4 V 电压源串联可以等效为一个44 V的电压源（注意电压源参考方向），1 Ω、2 Ω、20 Ω、2 Ω 共4 个电阻串联可以等效为一个25 Ω的电阻，等效电路图为图1-84（d）所示，。

受控源也可以进行等效变换：受控电压源与电阻的串联可以等效为受控电流源与电阻的并联，受控电流源与电阻的并联可以等效为受控电压源与电阻的串联，但转换过程中要特别注意不要把受控源的控制量丢掉。

【例1-19】　计算如图1-85（a）所示电路的电流i。

图1-85　例1-19 电路

解：利用电源等效变换，把受控电流源与电阻的并联等效为受控电压源与电阻的串联，受控电压源为5i×2＝10i，电阻为2 Ω，电路等效如图1-85（b）所示；2 Ω 与3 Ω 串联等效为5 Ω 电阻后与受控电压源的串联等效为受控电流源与电阻的并联，受控电流源为＝2i，电阻为5 Ω，如图1-85（c）所示；5 Ω 电阻与5 Ω 电阻并联等效为2.5 Ω 电阻，然后与受控电流源的并联等效为受控电压源与电阻的串联，受控电压源为5i，电阻为2.5 Ω，等效电路如图1-85（d）所示。列写的KVL 方程为

【例1-20】　计算如图1-86（a）所示电路的电压u。

图1-86　例1-20 电路

解：利用电源等效变换，把图1-86（a）中的2 A 电流源与5 Ω 电阻的并联等效为电压源与电阻的串联，电压源为2 A×5 Ω＝10 V，串联的电阻为5 Ω；受控电压源与12 Ω 电阻的串联等效为受控电流源与电阻的并联，受控电流源为，并联的电阻为12 Ω，等效电路如图1-86（b）所示。24 Ω 电阻与12 Ω 电阻并联的等效电阻为，与受控电流源并联后等效为受控电压源与电阻的串联，受控电压源为8×2.5u＝20u，串联的电阻为8 Ω，10 V 电压源与40 V 电压源串联等效为50 V 电压源。等效电路如图1-86（c）所示。列写出KVL 方程为

可得