电感元件是实际电感器的理想模型。把金属导线绕在磁芯上就会构成实际的电感器，该磁芯可以是磁性材料也可以是空气。电感器广泛应用在电子和电力系统中，如变压器、收音机中的振荡线圈等。电感器是一种储存磁场能量的电子元件。

图1-50 所示为电感线圈。当电流i（t）通过线圈时就会产生磁通Φ（t），如果忽略耗能等次要因素，在电路分析和计算中，就可以用电感元件替代实际电感器。

电感器的分类与测量见二维码1－9。

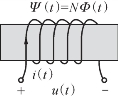
图1-50　电感线圈

1.电感元件及其伏安特性

电感元件的特性往往用其通过的电流i（t）和产生的磁通链Ψ（t）的关系来描述。如果一个二端元件在任一时刻，其上通过的电流与其产生的磁通链之间的关系可以由i－Ψ 平面上的一条曲线所确定，即

则称此二端元件为电感元件。此特性曲线称为韦安特性曲线，如图1-51（a）所示。在任何时刻，如果通过电感元件的电流i 与其磁通链Ψ 成正比，即i－Ψ 韦安特性是过原点的一条直线，则称该电感元件为线性定常电感元件，简称电感。如果不加说明，本书提到的电感都是指线性定常电感元件。电感元件的韦安特性曲线如图1-51（b）所示。

二维码1－9　电感器的分类与测量

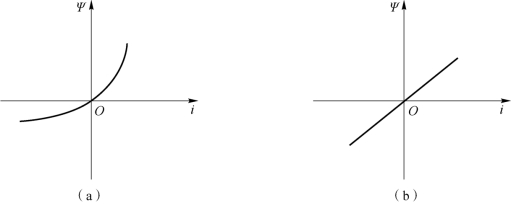
图1-51　电感元件的韦安特性曲线

（a）电感元件；（b）线性定常电感元件

电感的电路符号如图1-52 所示。

图1-52　电感的电路符号

通过电感元件的电流i 与其磁通链Ψ 之间的关系为

式（1-50）中，L 为电感的自感系数，对于线性定常电感元件来讲，L 是常数。电感的国际单位是H（亨），当电感量较小时，常用毫亨（mH）、微亨（μH）表示，它们之间的换算关系为

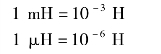
当电感线圈上有变化的电流时，电感中的磁通发生变化，从而在线圈两端感应电压。若电感的端电压u 和电流i 取关联参考方向，则根据电磁感应定律与楞次定律以及式（1-50），可得

式（1-51）称为电感元件VCR 方程的微分形式，表明电感元件的特点如下：

（1）电感两端的电压u的大小取决于其电流i的变化率，而与i的大小无关，因此，电感是动态元件；

（2）当i 为常数（直流）时，电流的变化率为零，所以电感的电压为零，即电感相当于短路；

（3）在实际电路中，电感的电压u 为有限值，因此，电感电流i 不能跃变，而是时间的连续函数。

在已知电感电流i（t）的条件下，用式（1-51）即可求出其电压u（t）。

例如，在L＝1 mH的电感上，施加电流为i（t）＝10sin（5t）A 时，其关联参考方向的电压为

电感电压的数值与电感电流的数值之间没有确定的关系，如将电感电流增加一个常量k，变为i（t）＝[k＋10sin（5t）]A 时，电感电压不会改变，这说明电感元件并不具有电阻元件在电压电流之间有确定关系的特性。

当电感两端的电压与其电流取关联参考方向时，如果电感上的电压已知，则电感上的电流为

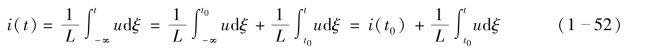
式（1-52）是电感元件VCR 方程的积分形式，其中i（t0）为电感电流的初始值，反映了电感初始时刻的储能状况，也称为初始状态。由式（1-52）可知，电感元件有记忆电压的作用，故称电感为记忆元件。在任意时刻t，电感电流的数值i（t），要由从－∞到t 时刻之间的全部电压来确定，即此时刻以前在电感上的电压都对t 时刻的电感电流有一定的贡献。这与电阻元件的电压或电流仅取决于此时刻的电流或电压完全不同。

当电感两端的电压u 与电流i 方向为非关联参考方向时，电感元件VCR 方程的微分和积分表达式前都要加负号，即

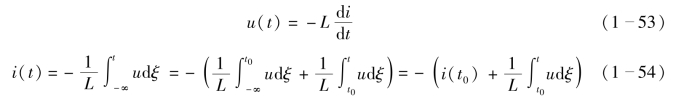
【例1-11】　已知L＝0.5 mH的电感电压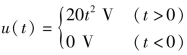，试求电感电流i（t）。

解：根据电感元件VCR 方程的积分形式得(www.daowen.com)

（1）当t>0 时，

（2）当t<0 时，i＝0 A。

2.电感的功率和能量

电感的记忆特性是其储存能量的表现，电感线圈上通电流，线圈会感应磁场并储存磁场能量。当电感电压u 与其电流i 取关联参考方向时，电感吸收的功率为

式（1-55）表明电感充放电的情况如下：

（1）当电流增大且i>0 时，，则u >0，线圈中的磁通链Ψ 增加，p >0，此时电感吸收功率；

（2）当电流减小，且i>0 时，，则u<0，线圈中的磁通链Ψ 减小，p >0，此时电感发出功率。

从以上分析可以看出，电感能在一段时间内吸收外部供给的能量，并将其转化为磁场能量储存起来，在另一段时间内又可以把能量释放回电路，因此电感元件是无源元件和储能元件，且它本身并不消耗能量。

在任意t 时刻，电感的储能是对其功率的积分，即

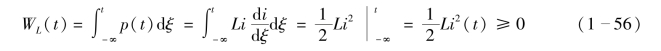
式（1-56）表明电感储能的特点如下：

（1）电感的储能只与当时的电流值有关，电感的电流不能跃变，反映了储能也不能跃变；

（2）电感储存的能量一定大于或等于0。

3.电感的串联与并联

1）电感的串联

如图1-53 所示，对于n 个电感串联的二端网络，就其端口特性而言，对外电路可以等效为一个电感。

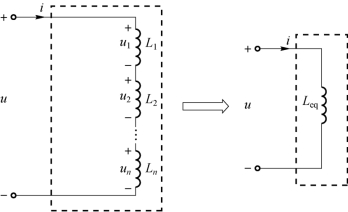
图1-53　电感的串联及其等效电路

（a）电感的串联；（b）等效电路

在图1-53（a）所示电路中，根据KVL 和电感的电压电流的关系，有

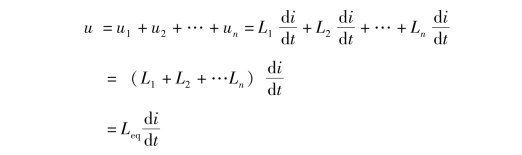
因此，串联电感电路的等效电感与各电感的关系式为

由式（1-57）可知，n 个串联电感的等效电感值等于各串联电感值之和。

2）电感的并联

如图1-54 所示，对于n 个电感并联的二端网络，就其端口特性而言，对外电路可以等效为一个电感。

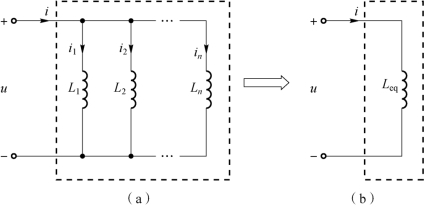
图1-54　电感的并联及其等效电路

（a）电感的并联；（b）等效电路

如图1-54（a）所示，根据KCL 及电感的电压与电流的关系式，有

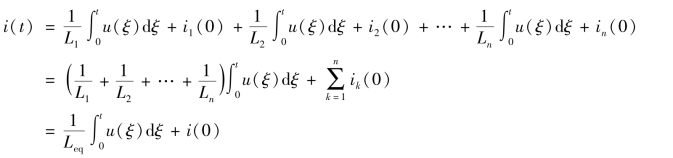
因此，并联电感电路的等效电感与各电感的关系式为

由式（1-58）可知，n 个并联电感的等效电感值的倒数等于各并联电感值的倒数和。

当两个电感并联，即n＝2 时，等效电感值为