电容元件是实际电容器的理想模型。电容器是由绝缘体或电介质材料隔开的两个金属体组成的，应用非常广泛，种类也很多，如空气电容、陶瓷电容、纸电容、云母电容、电解电容和贴片电容等。实际的电容器能够聚集电荷，在电荷聚集的过程中伴随着电场的形成。在外电源作用下，电容器两个极板上分别带有等量的异号电荷，撤去电源，极板上的电荷仍可长久地聚集下去，是一种储存电能的部件。充电和放电是电容器的基本功能，另外，电容器还具有滤波、去耦等功能。如果忽略电容器在实际工作中的漏电流和磁场的影响等次要因素，在电路分析和计算中就可以用电容元件替代电容器。

电容器的分类与测量见二维码1－8。

二维码1－8　电容器的分类与测量

1.电容元件及其伏安特性

电容元件是表征产生电场、储存电场能量的元件。电容元件上的电荷和电压的关系往往用来反映电容的储能特性。

如果一个二端元件在任意时刻，其电荷与电压之间的关系由q－u 平面上一条曲线所确定，即

则称此二端元件为电容元件。此特性曲线称为库伏特性，如图1-44 所示。如果在任意时刻，电容元件极板上的电荷q 与电压u 成正比，即特性曲线是通过q－u 平面上原点的一条直线，如图1-45 所示，则称之为线性时不变电容。线性电容元件简称电容，其电路符号如图1-46 所示。

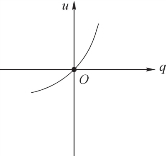
图1-44　电容元件的库伏特性曲线

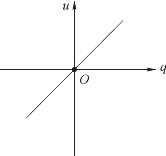
图1-45　线性电容元件的库伏特性曲线

电容的大小用C 表示，其表达式为

图1-46　线性电容元件的电路符号

或

式（1-39）中，电容C的单位是法拉，简称法（F），常常用微法（μF）和皮法（pF）表示。它们之间的换算关系为

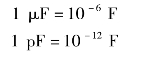
当电容两端的电压发生变化时，聚集在电容极板上的电荷也发生相应的变化，连接电容的导线上就有电荷的移动，即有电流流过；如果电容两端的电压没有发生变化，则聚集在电容极板上的电荷也不会发生变化，即不会有电流流过。

当电容两端的电压与其上流过的电流取关联参考方向时，由于和q＝cu，电容两端的电压与其上通过的电流的关系式（VCR）为

式（1-41）为电容VCR 方程的微分形式，表明电容元件的特点如下：

（1）在任一时刻电容电流i的大小与电压u的变化率成正比，与u的大小无关，因此，电容是动态元件；

（2）对于直流电路（u 为常数），电压的变化率为0，所以电容的电流为0，即在直流电路中，电容相当于开路，因此，电容有隔直流、通交流的作用；

（3）在实际电路中通过电容的电流i 为有限值，所以电容电压u 是时间的连续函数。

根据式（1-41），如果电容上的电流已知，则电容两端的电压为

式（1-42）是电容VCR的积分形式。其中，uC（t0）为电容电压的初始值，反映了电容初始时刻的储能状况，也称为初始状态。由式（1-42）可知，电容具有记忆电流的作用，故称电容为记忆元件。在任意t 时刻，电容电压的数值uC（t），都要由从－∞到t 时刻之间的全部电流iC（t）来确定，即此时刻以前流过电容的电流都对t 时刻的电压有一定的贡献。这与电阻的电压或电流仅仅取决于此时刻的电流或电压完全不同。

当电容两端的电压与电流方向为非关联参考方向时，电容VCR 方程的微分和积分表达式前要加负号，即

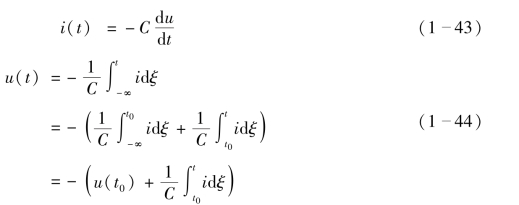
2.电容的功率和能量

对电容施加电压，极板之间会产生电场，并储存电场能量。当电容电压u 与其电流i 取关联参考方向时，电容吸收的功率为

式（1－45）表明电容充放电的情况如下：

（1）当电容充电且u>0 时，，则i>0，电容器极板上的电荷q 增加，p>0，电容吸收功率；

（2）当电容放电且u>0 时，，则i<0，电容器极板上的电荷q 减小，p<0，电容发出功率。

从以上分析可以看出，电容能在一段时间内吸收外部供给的能量，并将其转化为电场能量储存起来，另一段时间内又把能量释放回电路，因此电容是无源元件和储能元件，且它本身并不消耗能量。

在任意时刻t，电容的储能为

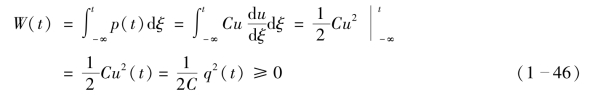
式（1-46）表明电容储能的特点如下：(www.daowen.com)

（1）电容的储能只与当时的电压值有关，电压不能跃变，即储能不能跃变。

（2）电容储存的能量一定大于或等于0。

【例1-10】　已知100 μF的电容两端的电压波形如图1-47（a）所示，当其两端电压与其上通过的电流为关联参考方向时，试计算电容上流过的电流iC（t），并画出波形图。

解：根据图1-47（a）中电容电压的波形图，按照时间分段来进行计算：

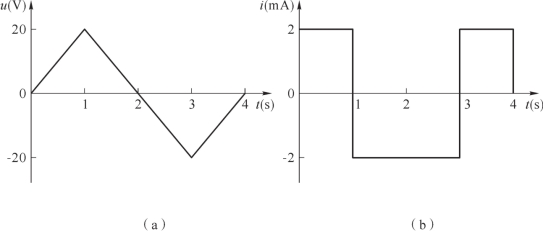
图1-47　例1-10 电容电路的波形图

（a）电压；（b）电流

（1）当0 s≤t≤1 s 时，u（t）＝20 t，根据可以得到

（2）当1 s≤t≤3 s 时，u（t）＝（－20t＋40）V，可以得到

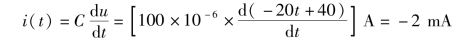
（3）当3 s≤t≤4 s 时，u（t）＝（20t－80）V，可以得到

根据以上计算结果，电容电流的波形图如图1-47（b）所示。

3.电容的串联与并联

和电阻的串并联相同，电容的串并联也可以进行等效。

1）电容的串联

如图1-48 所示，n 个电容串联的二端网络，就其端口特性而言，对外电路可以等效为一个电容。

在图1-48（a）所示电路中，根据KVL 可知

代入各电容的电压、电流关系式，可得

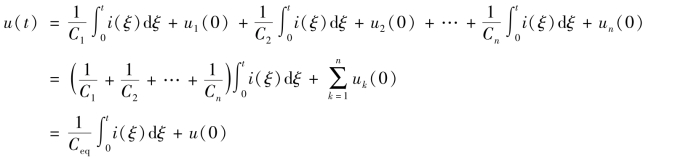
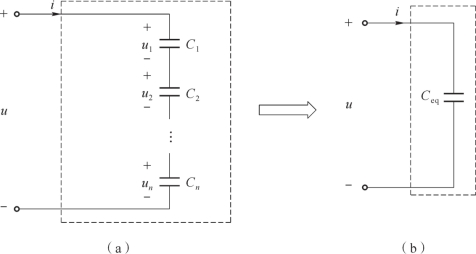
图1-48　电容的串联及其等效电路

（a）电容的串联；（b）等效电路

因此，串联电容电路的等效电容与各电容的关系式为

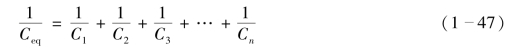
由式（1-47）可知，n 个串联电容的等效电容值的倒数等于各串联电容值的倒数之和。

当两个电容串联，即n＝2 时，等效电容值为

2）电容的并联

如图1-49 所示，n 个电容并联的二端网络，就其端口特性而言，对外电路可以等效为一个电容。

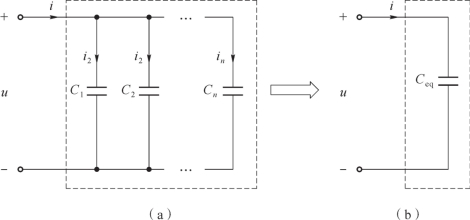
图1-49　电容的并联及等效电路

（a）电容的并联；（b）等效电路

在图1-49（a）所示电路中，根据KCL 可知

代入各电容的电压、电流关系式，可得

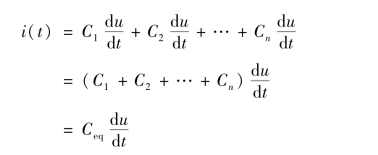
因此，并联电容电路的等效电容与各并联电容之间的关系式为

由式（1-49）可知，n 个并联电容的等效电容值等于各并联电容的电容值之和。