调速器工作特性与调速器的结构和设计参数有关，前已说明，作为初步设计可以采用静力学计算，进一步的研究则需进行动态过程的分析，由于篇幅所限，本书只介绍飞锤式调速器的静力计算方法。

在计算前，先对调速器进行简化，简化后的物理模型如图7-11a所示。尽管飞锤形状较为复杂，但可把它作如下简化：求出飞锤的质心，把飞锤的质量集中在其质心处并置于无质量的L形杠杆的一端上，L形杠杆能绕飞锤销中心A转动，其另一端与调速套筒接触，因此飞锤在离心力作用下，可经L形杠杆推动调速套筒轴向移动，调速套筒的另一端有等效的调速弹簧力作用，等效调速弹簧是根据调速器调速弹簧的结构和位置尺寸，将其作用力转化到调速套筒的轴向位置上的假想弹簧。计算中，忽略运动件的摩擦力，由于飞锤对称，故飞锤重力对调速套筒的作用相互抵消。因此，经简化后剩下的力只有两个，即飞锤离心力F_c（若再进一步换为套筒的轴向分力即为式（7-1）所示的飞锤支持力F）和等效弹簧的恢复力F_E（即式（7-3）所示的E）。柴油机转速一定时，可算出F_c和F_E的数值。在F_c和F_E的综合作用下，调速套筒处于某一轴向平衡位置Z，而调速套筒经杠杆与喷油泵齿杆连接，因此可以通过相应的几何关系进一步计算出齿杆位移S随转速n的变化关系，即调速器的工作特性或调速特性。

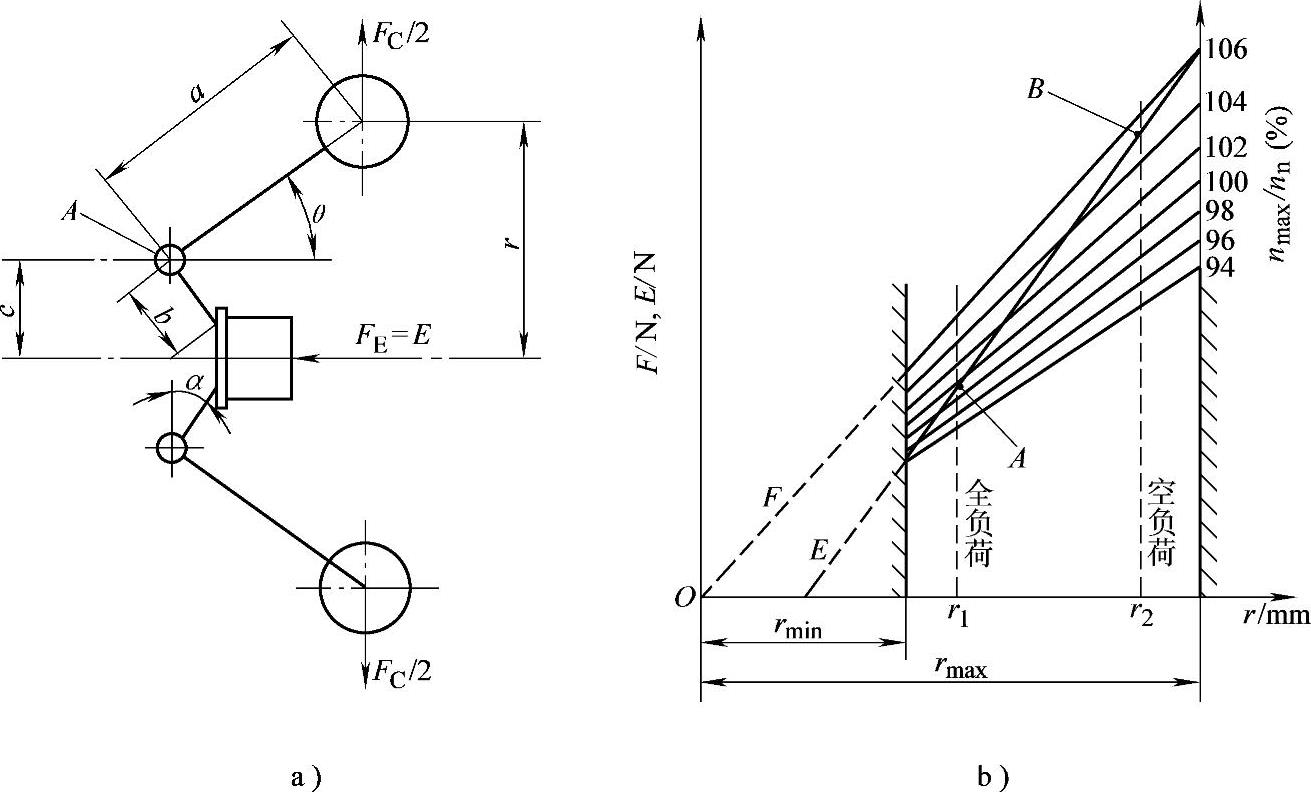
图7-11 调速器的静力学计算

a）简化模型 b）静力学平衡图表

计算时离心力F_c可按下式求得：

F_c=0.001Mω²_pr （7-12）

式中，F_c为离心力（N）；M为飞锤总质量（kg）；r为飞锤质心旋转半径（mm）；ω_p为调速器轴的角速度（rad/s），它可由调速器转速求得。

弹簧恢复力F_E则与式（7-3）相同，即

F_E=E=E₀+KZ（7-13）

式中，K为等效调速弹簧刚度（N/mm）；Z为调速套筒位移（mm）；E₀为等效调速弹簧预紧力（N）。

再按图7-11a求出飞锤质心径向位移与调速套筒位移的几何关系，由于设计调速器时，L形杠杆臂的夹角一般取为90°，故有α=θ，设飞锤处于合拢最内位置（r=r_min）时，调速套筒位移Z₀=0，则飞锤径向位移Δr=r-r_min与相应调速套筒位移Z之间的关系，可按以下方法求出。

当转速不变时，对飞锤销中心A存在力矩平衡，有

F_cacosθ=F_Ebcosα

由于α=θ，可得(www.daowen.com)

按虚位移原理，有

F_EZ=F_cΔr

将式（7-14）代入上式后，即得

式（7-14）中，F_E=F_ca/b即相当弹簧的恢复力E，也应等于飞锤离心力F_c转化到调速器套筒方向的支持力F，因为在稳定工况下，两者应当相等（参见式（7-4）和式（7-12））。由此可得

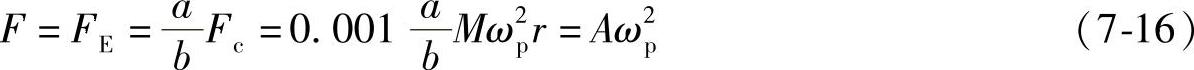
这样，也就求出了前面式（7-1）中的惯性力系数A=0.001Mra/b，由此可见，它与飞锤质量M和飞锤质心的回转半径r有关。

为了对于调速器静力平衡有一个形象明确的概念，可以用图7-11b所示的静力学平衡图来加以说明。

对于不同转速，支持力F与飞锤半径r之间的关系是一组通过坐标原点的直线族。由于结构的限制，r可能变化的范围只是r_min～r_max。

为了把弹簧恢复力F_E=E也画在同一图上，可将原为调速套筒位移Z函数的E转换成飞锤位移Δr=r-r_min的函数，即将式（7-15）代入式（7-13）后，可得

式中，bK/a为图7-11b中弹簧恢复力E曲线的斜率。调速器操纵杆位置改变，代表恢复力E的斜线在图中平行移动。例如，由调速器结构确定出全负荷和空负荷时最高转速的飞锤位置为r₁和r₂，由式（7-15）也就确定了调速套筒位移Z₁和Z₂，相应得出齿杆位移S₁和S₂（对应图7-6中的C点和D点）。如图7-11b所示，曲线E和曲线族F在A点（全负荷）和B点（在空负荷）相交，对照右边纵坐标轴上的n_max/n_n值，可查得调速器稳定调速率约为5%。