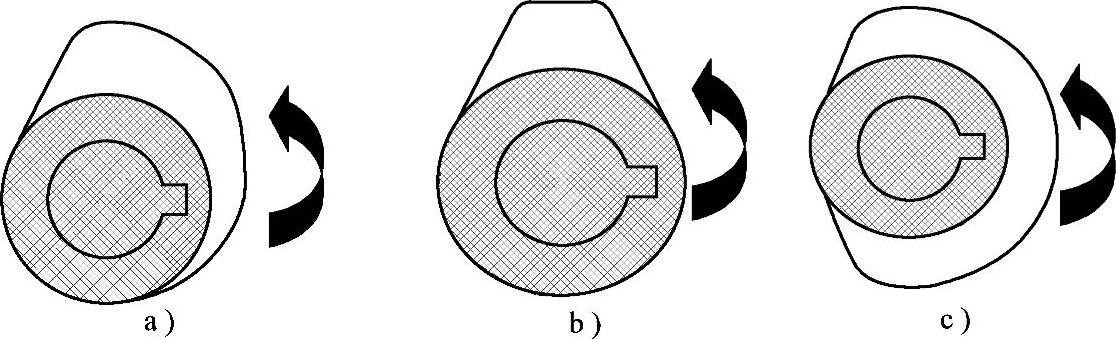
图5-20 三种典型的切线凸轮

a）单向切线凸轮 b）双向切线凸轮 c）扇形切线凸轮

在传统的柱塞式喷油泵中，装在柱塞尾部的弹簧盘是由弹簧经过挺柱的滚子压紧在凸轮轴的凸轮表面上的（图5-1、图5-2、图5-5～图5-8），因此柱塞的运动完全受到凸轮旋转的控制，柱塞的最大升程也就是凸轮的最大升程，凸轮的升程与几何形状（型线）对柱塞的运动规律与喷油泵的供油规律有着重要的影响。凸轮型线的各类很多，目前在中小功率柴油机领域使用最多的为如图5-20所示的切线凸轮：其中，图5-20a所示为单向切线凸轮，又称T型凸轮，系不对称凸轮，其凸轮工作段为一条与基圆相切的直线，它只能用于某一固定旋转方向，但回程比较平缓，对提高零部件的寿命与降低工作时的噪声比较有利；图5-20b所示为双向切线凸轮，又称G型凸轮，由于它两个侧面均为对称布置的切线，故可以实现双向旋转；图5-20c所示为扇形凸轮，它也是对称凸轮，不过凸轮外圆周很长，使柱塞在较大的凸轮转角内，一直保持在上止点处，只是在工作时作一次短时间的往复（吸油和泵油）运动，这样可以防止柴油机发生意外反转，但因缩短了柱塞顶部空腔的充油时间，故目前采用的不如前面的T型和G型凸轮普遍。

图5-21所示为两种典型凸轮（用于P7型喷油泵上的T型和G型凸轮）升程和速度曲线的比较。

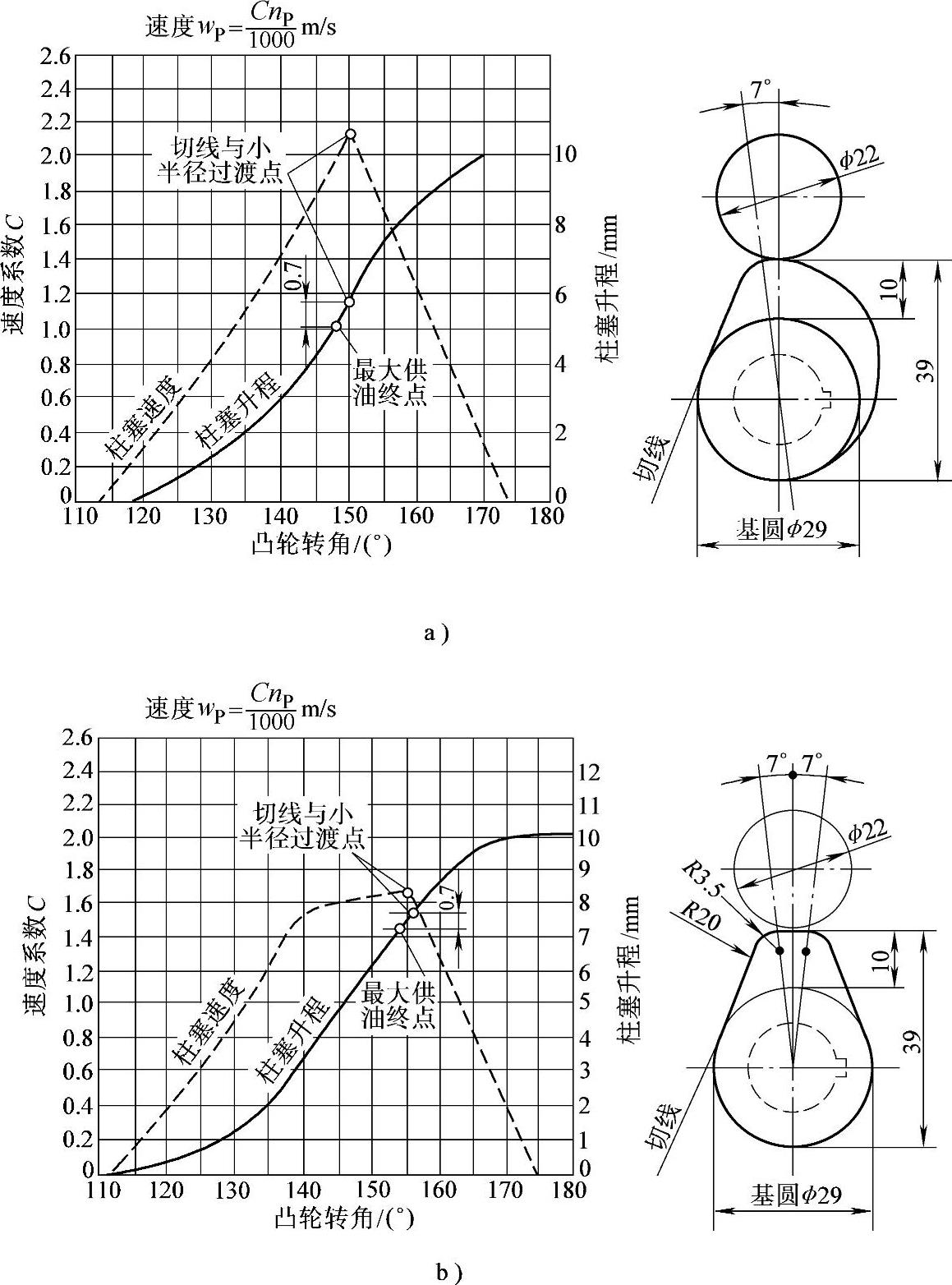
图5-21 两种典型凸轮升程和速度曲线的比较

a）P7泵T型凸轮 b）P7泵G型凸轮

由图5-21a可见，T型凸轮的柱塞速度曲线近似三角形，符合先缓后急的理想供油规律，使滞燃期内只喷入少量的燃油，确保柴油机能平稳地并以较小的燃烧噪声运行，着火后，又能以较高的供油速率将燃油供给喷油器，使其尽快喷完，从而把喷油持续角控制在一定范围内，保证柴油机获得良好的性能。但在相同的平均供油速率的条件下，柱塞的最高速度比G型凸轮高，因此，最高供油速率以及由此引起的最高泵端压力要比G型凸轮高。

由图5-21b可见，G型凸轮的柱塞速度曲线近似为梯形，故又称等速凸轮，这种凸轮在工作时，整个供油延续角基本上都在等速段，因此，供油速率在开始时就较高，对噪声不利，但在相同的平均供油速率下，柱塞最高速度低于T型凸轮，因此，最高供油速率及最高泵端压力低于T型凸轮。

在图5-21所示的凸轮升程、速度曲线中，为了便于比较各种凸轮形线对柱塞速度的影响，速度曲线纵坐标用基准速度C（又称速度系数）表示，它是喷油泵转速为1000r/min时的速度值，这样对应任一柴油机转速n_P均可方便地求得柱塞供油速度为w_P=Cn_P/1000（m/s），对中小功率柴油机用的喷油泵，C的最大值一般应控制在3.0m/s以下。(www.daowen.com)

前已说明，凸轮全升程，即最大升程就是柱塞的最大升程h_max，对比如图5-4所示的关系A=h₁+h₂+h₃+h₄可知，A即为h_max，再将h₁+h₂两项合并为h_ps，并令h₃=h_e，h₄=h_r，则有

式中，h_e为有效行程；h_ps为预行程；h_r为剩余行程。

取h_max与h_e之比为m₂，即h_max=m₂h_e。对于自然吸气柴油机，m₂在4.0～7.0之间，对于增压柴油机m₂在3.0～5.0之间，增压度越高，m₂取越小的值。这样，在按式（5-6）计算柱塞直径d_p并确定h_e以后，也可根据以上关系确定h_max，至于预行程h_ps与剩余行程h_r在h_max中如何分配的问题，则取决于对供油速率的要求。前已指出，柱塞的运动规律主要是由凸轮型线确定的，但同一种柱塞即使用同一根凸轮轴，通过不同的调整，亦可得到不同的柱塞运动速度以及不同的供油速率和供油规律。通常，当循环供油量一定时，为了缩短供油持续期，应尽可能提高供油速率，即将有效行程h_e的终点调整在距最大速度点0.3mm处，这时既保证了较高的供油速率，使供油持续期控制在较窄的凸轮转角范围内（在高速柴油机中，通常小于10°，见图3-3中的AB段），又防止了挺柱与凸轮顶部圆弧相接触，造成表面接触应力过大（最大允许值为1900～2000MPa）。在实际喷油泵上预行程的大小可通过改变挺柱体的高度（如A型泵）或柱塞套法兰下的垫片厚度（如P型泵）来加以调节。

在上述切线凸轮中存在的问题就是切线与圆弧交接处由于凸轮的曲率半径由无穷大突然减小为R=3.5mm左右的小圆弧（图5-21），致使这一部位与滚轮的接触应力明显增大，加剧了局部磨损，同时柱塞运动的加速度也从最大的正值，突变成最大负值，形成一条不连续的加速度曲线（见图5-22中的曲线A_a-B_a-C_a-D_a，其中B_a-C_a段表示由最大正加速度B_a突然跳到最大负加速度C_a）。此外，在最大负加速度出现的瞬间，容易产生滚轮与凸轮脱开现象，从而限制了喷油泵转速及供油速率的进一步提高。

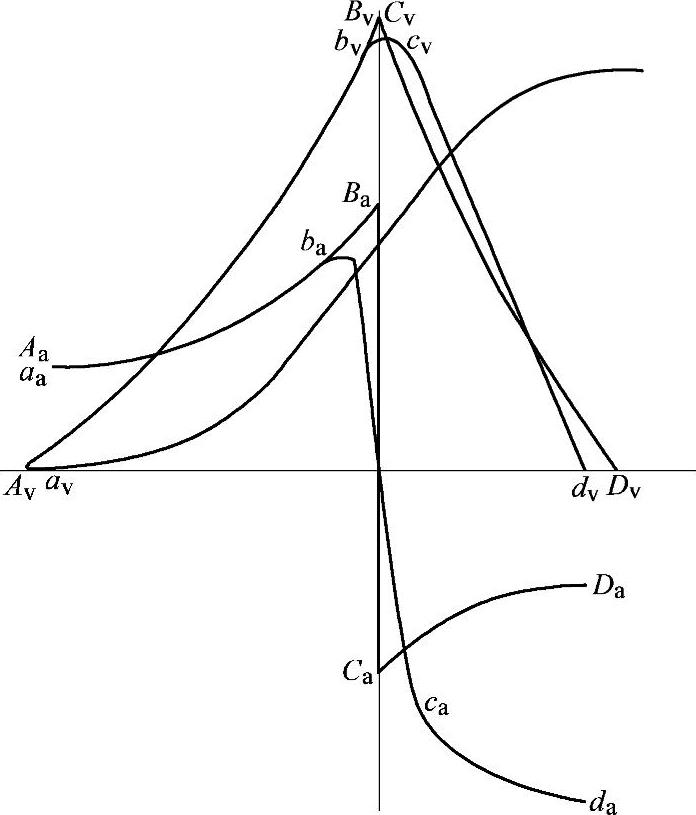
图5-22 两种凸轮型线过渡段的运动特性比较

A_a-Ba-Ca-Da为切线-小圆弧凸轮的加速度曲线A_v-Bv-Cv-Dv为切线-小圆弧凸轮的速度曲线a_a^-ba-ca-da为切线-函数凸轮的加速度曲线a_v^-bv-cv-dv为切线-函数凸轮的速度曲线

为了进一步克服上述缺陷，近年来，国内外也开始采用函数凸轮作为过渡段来与切线衔接，即开发了所谓切线-函数凸轮。这种凸轮可使切线与函数曲线过渡部分的曲率半径逐渐减小，这就改变了切线-小圆弧凸轮上加速度曲线的不连续性，形成了一条连续的加速度曲线（见图5-22中的曲线a_a-b_a-c_a-d_a），凸轮受力薄弱环节处的接触应力也显著降低，从而可提高许用泵端压力。

此外，函数凸轮过渡段的负加速度走向也与柱塞弹簧的压紧力大体一致，可以保证弹簧压力不过度的情况下，柱塞与挺柱-滚轮从动件的可靠接触。函数曲线的形式很多，可以采用三角函数（正弦或余弦）、多项幂指数曲线等。有关这方面的内容，读者可以参考凸轮设计方面的专著，本书因篇幅限制，不再赘述。