喷油过程计算时，要将实际燃料供给系统适当加以简化，抓住其结构与工质（燃油）性质的主要特点，应用已经掌握的科学知识，建立相应的物理和数学模型（简称计算模型），对整个系统数学求解，得到包括供油压力（泵端）、喷油压力（喷嘴）、针阀升程、喷油量与喷油规律等在内的一系列参数，从而达到能够预测喷油过程的基本特性，研究各参数变化对喷油特性的影响，解决燃料供给系统与整机匹配中相关问题等目的。利用燃料供给系统的计算结果，结合缸内过程的模拟计算，还能对柴油机的喷雾、混合气形成与燃烧过程进行深入的研究。

柴油机燃料供给系统计算时所依据的基本理论仍然是：基于质量守恒定律的流体连续性方程，基于动量定理的运动微分方程以及基于能量守恒定律的能量微分方程。尽管这些计算的理论与公式已早为人知，但只有在电子计算机广为应用以后，才能得到实用推广并发展到今天比较完善的程度。

燃油的可压缩性是在燃料系统计算中必须考虑的一个因素。它可以用压缩性系数即单位压力变化引起的容积相对变化β来表示，即

式中，负号表示压缩，其值随压力而变（随压力的增加而减小），当压力变化为0～50MPa时，柴油的β=（4～6.5）×10^-4（MPa）-1。压缩系数β的倒数称为燃油的弹性模量E，即

当压力变化为0～50MPa时，柴油的E=（1.5～2.5）×10³MPa。知道了E和燃料的密度ρ以后，即可得出声音在燃油中的传播速度，即

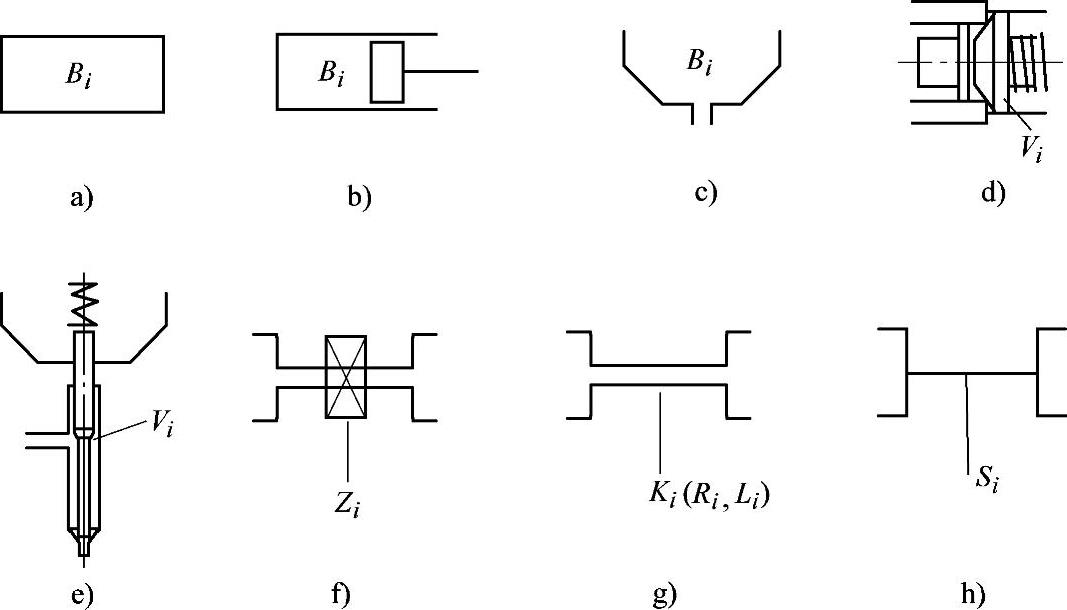
图3-7 组成液力装置各单元的示意图

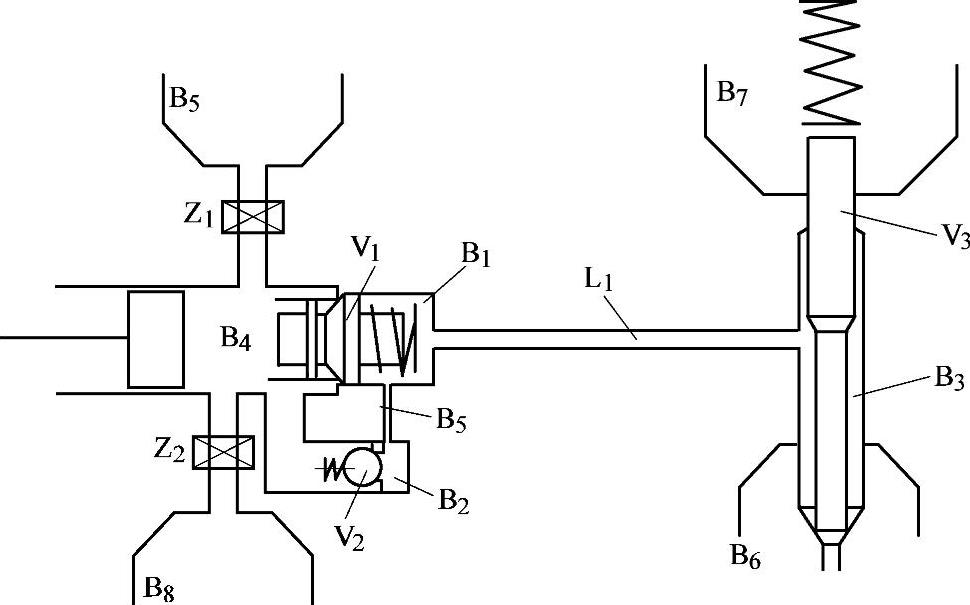
图3-8 泵-管-嘴燃料供给系统的计算模型

以后还将说明声速表达式本身就是描述燃油可压缩性的物态方程。柴油机燃料供给系统也像所有液力装置一样，由许多单元组成，其简图如图3-7所示。图中：B表示各种容积，图a为封闭式容积，图b为强制改变式容积，图c为开式（与大气相通）容积；V表示各种阀门，图d为泵端出油阀或球阀，图e为喷油嘴针阀；Z表示强制开闭式油道（图中为f）；K表示截面积不变的通道，例如高压油管，其中R表示短管，L表示长管（图中为g）；S表示精密偶件的微小缝隙（图3-7h）。所有符号的下标i表示该类元件在燃料供给系统中的序数。如图3-8所示则为由部分上述单元组成的采用等压式出油阀的传统的泵-管-嘴燃料供给系统的计算模型，由于没有考虑各部分的泄漏，故图中未出现“S”。

在对整个系统计算时，需找出以上各个元件的数学表达式以及它们之间相互关系，其中对于各类容积（B）应采用连续性方程，例如对于柱塞顶部空间B₄，应写为

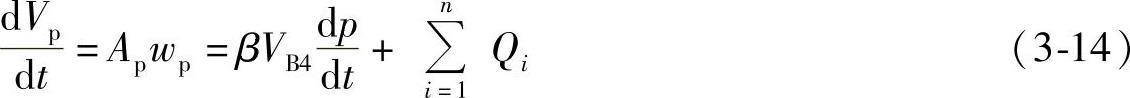
式中，左边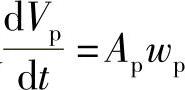即为几何供油率，由喷油泵结构参数（凸轮型线与柱塞面积）给出，右边第一项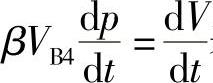表示容积中燃油在高压下于单位时间内受到的压缩量。集中容积中压力的变化实际上也是压力波不断反射叠加的结果，但由于这些容积几何路程很短，可以略去压力波传递的时间，认为容积内同一瞬间各处压力都是相等的，p即代表整个容积的压力；右边第二项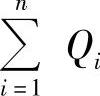表示单位时间内经各个连接通道与阀门（Z，V）流出该容积的流量的总和，其中各Q_i的表达式为

式中，Δp_i为连接通道两端容积内的压力差，（_μf）i为有效流通截面（mm²），μ为流量系数，f对于截面不变的通道为定值，但对于强制开闭的通道Z₁与Z₂以及出油阀V₁则为变数。

对于喷油器的压力室B₃也可以采用类似的数学表达式，即

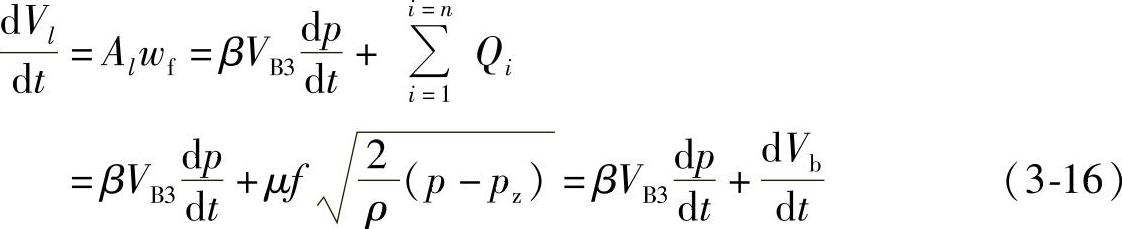
这里左项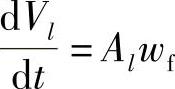为单位时间内经高压油管流入喷油器的燃油量（A_l为高压油管内流动面积，w_f为管内燃油流速）；右边第一项为压缩项，第二项为单位时间内经喷油嘴喷入气缸中的燃油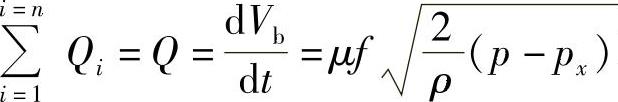，即喷油率，式中_μf为喷油嘴的有效流通截面，p为喷油压力，p_x为气缸内的背压。

当喷油泵出油阀V₁和针阀V₃运动时，其流通截面均随出油阀升程h₁或针阀升程h₃而变，它们的运动规律则应按相应的动量微分方程计算：

这里m_i表示出油阀或针阀的质量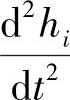，表示它们的加速度，F_i表示作用在出油阀或针阀上的外力，包括由于阀门两侧的压力差或承压面积差造成的力、与阀门运动速度成正比的阻尼力以及复位弹簧的作用力，等等。

在列出各集中容积的连续性方程时，还要注意对计算过程中时间上各个阶段进行划分，例如当出油阀V₁未打开而进出油孔Z₁、Z₂已关闭时或喷油器未打开时，B₄与B₃相当于图3-7b的情况，这时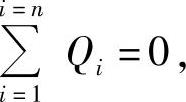柱塞上行时的供油率或喷油器进口处的燃油流量，只用来对系统内的燃油进行压缩，即有

当柱塞已停止供油（A_pw_p=0）或喷油器不再进油（A_lw_f=0）而出油阀或针阀尚未关闭时，燃油又会由于卸压后的膨胀作用继续经出油阀或针阀流出，即有

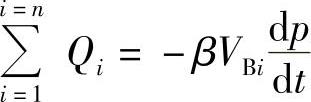
总而言之，在对柴油机燃料供给系统进行数值模拟计算时，必须要仔细对系统各部分进行分解并加以适当简化，在全面分析各部分相互关系的前提下，列出这些单元在各个供油与喷油阶段时的计算公式。以上介绍的只是有关集中容积的连续性方程与运动件的运动方程的计算方法，目的是讲清计算的基本概念，并没有列出各部分计算中的所有细节。

这里我们还要着重介绍一下连接喷油泵与喷油器的高压油管对喷油过程的影响，这是柴油机燃料供给系统计算中十分关键的部位，因为不论是泵-管-嘴系统中的长管（L）或短管（R），还是共轨系统中由高压油轨通往各喷油器的油管，均不能作为集中容积来处理，因为在同一时间内油管各处压力并不相等，而且是以压力波形式在各点之间进行传播的，通常我们是将其当作为可压缩流体的一维不定常流动来处理的。为此，必须依靠流体连续性方程与动量方程来确定声速的表达式并建立“波动”方程，其原理如下所述：

在图3-9a中，在管道截面上1-1处，有一个假想面积为A（等于管道内流动面积）的柱塞，以速度u+du向前运动，使介质受到压缩，压力从p增加为p+dp，并以声速a向前传播，这时作用在截面上的力为dF=Adp，经过时间dt以后，压力波前锋传至截面2-2处，其间的距离为L=adt，这时在原来波峰面上压力由p增加为p+dp，速度由u增加为u+du，这一小段流体L=adt，也因此受到压缩，压缩量为dL=-dudt，密度则由ρ变为ρ+dρ。根据质量守恒定律，这段液柱在压缩前后的质量应当相等，即有

m=ALρ=A（L+dL）（ρ+dρ）

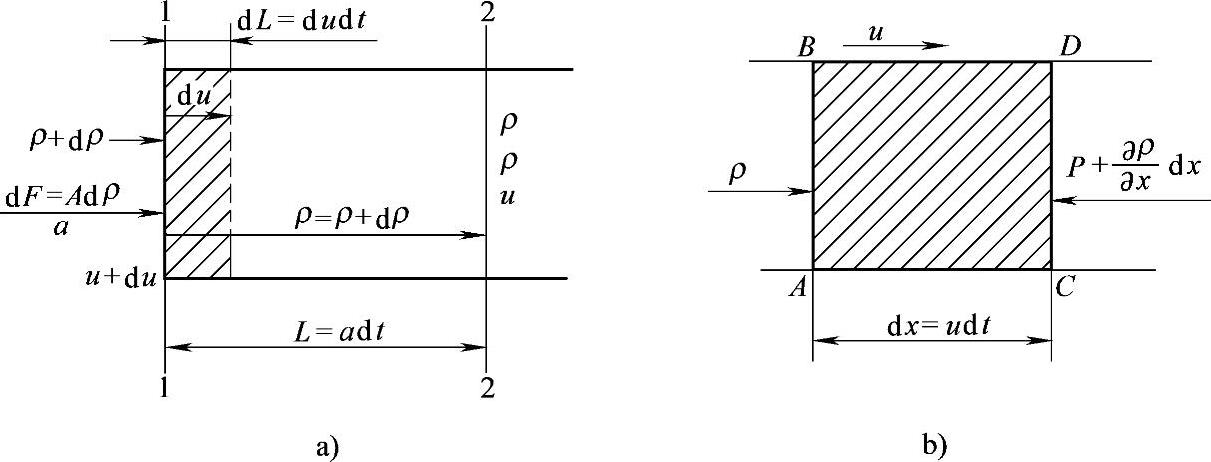
图3-9 高压油管内的液力过程

a）声速的确定 b）波动方程的建立

展开、化简并略去高阶无穷小量dLdρ后可得

Ldρ+ρdL=0 （3-18）

另外，根据牛顿第二定律，作用在上述这段流体两端作用力之总和应当等于这段流体质量乘以其加速度，即有

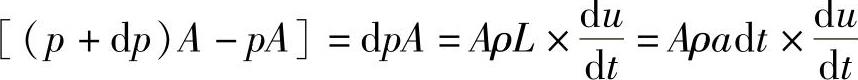
故有 dp=ρadu

将式（3-19）与式（3-20）相乘可得

再根据式（3-12）的燃料弹性模量E的定义，有

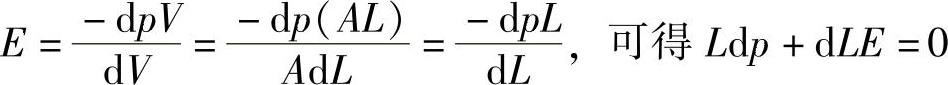
代入式（3-18）后，可得

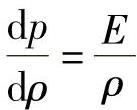
因此，推导的声速表达式与式（3-13）所表达的完全一致，即有

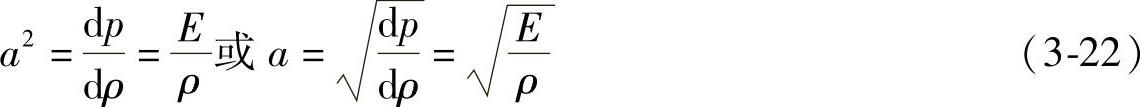
上述声速的表达式实际上就是描述燃油可压缩性的物态方程。在此基础上，可进一步根据质量守恒与牛顿第二定律，求出压力波在管道中传播的规律。为此，在如图3-9b所示管道中取一小段控制容积ABCD，其长度为dx=udt，（u为燃油在管内的流速）若不考虑管壁流动损失，则按牛顿第二定律，可以列出它的运动方程如下：

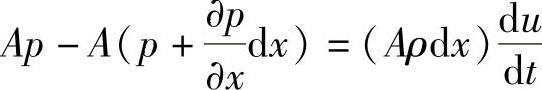
其中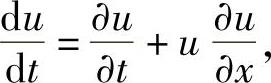代入上式后，可得

由于管道内燃油流速u要比声速a小很多，一般u≤40m/s，而a在1300～1500m/s之间，因此反映流速及其变化的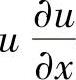项与反映声速数量级的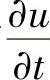（因压力波传递而引起的速度变化）相比可以略去，即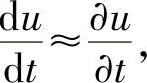故上式又可简化为

同时按连续流动方程，在dt时间内经AB截面流入控制容积的质量为Aρudt，经CD截面流出控制容积的质量为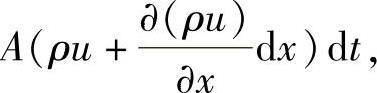这就引起控制容积中密度的变化，而由密度变化引起的质量变化为

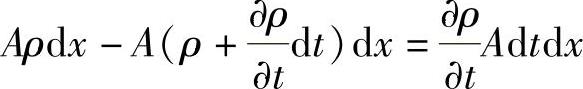
但根据质量守恒定律，上述变化应等于流入与流出控制容积质量之差，即

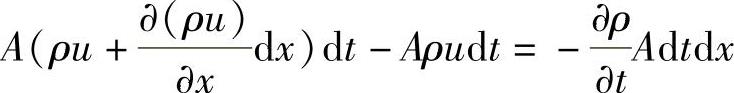(www.daowen.com)

展开整理后即有

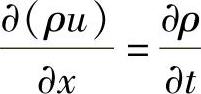
由于同样的原因，略去比其他项小很多的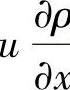项以后可得

此外，在声速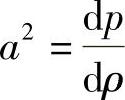的公式（式3-21）中，将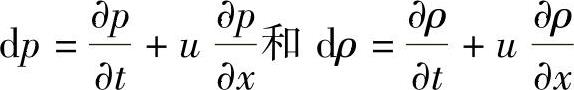代入并略去含u的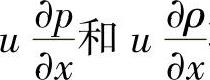项以后，可得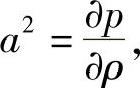再代入式（3-26）以后可得

将式（3-24）与式（3-27）分别对x和对t微分，再相减以后即可得出

或

式（3-28）和式（3-29）就是用来求解管道中压力波或速度波传播的波动方程。它们均为两阶双曲线型的偏微分方程，它们中任一个均与式（3-24）与式（3-27）构成的一阶微分方程组式（3-30）是等价的，只是表达的方式不同而已：

对于波动方程的通解，一般是采用达朗贝尔（D′ALembert）的形式，即

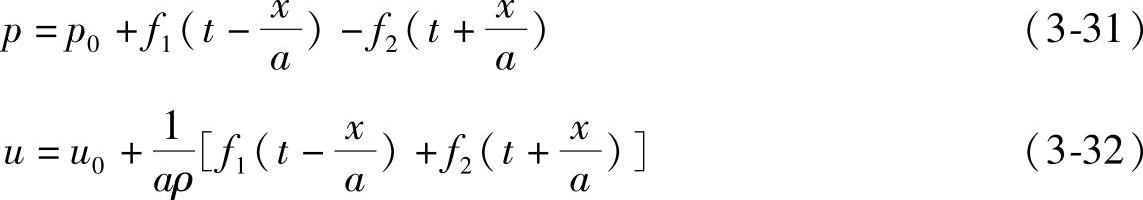
式中，p₀和u₀分别为压力波传播前管内的初始压力和速度。由于在两次喷射之间，系统内的燃油流动与压力波动已停止，故u₀=0，p₀为系统残余压力。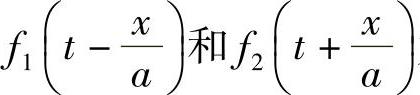为偏微分方程通解中的任意函数，取决于高压油管两端即泵端与嘴端的边界条件。f₁或f₂函数表示的是一个以速度为a的波动传播过程，它们的单位为压力单位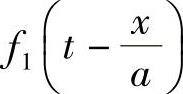，表示前进压力波（由喷油泵传向喷油嘴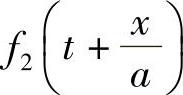），表示反射压力波（由喷油嘴返回喷油泵）。

如图3-10所示，即为喷油泵压力向喷油嘴传播过程以及前进压力波与反射压力波相互叠加的示意图。

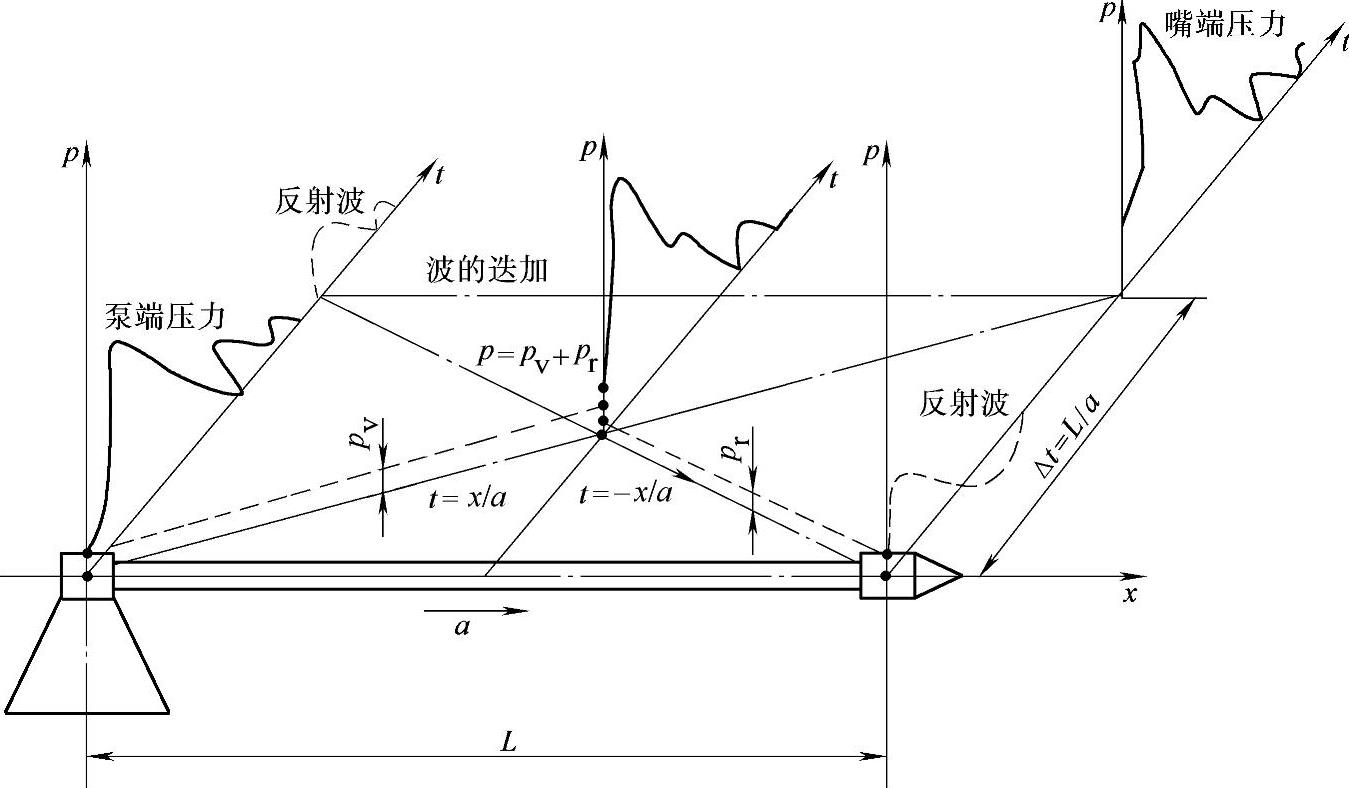
图3-10 柴油机燃料供给系统中压力波传播与叠加示意图

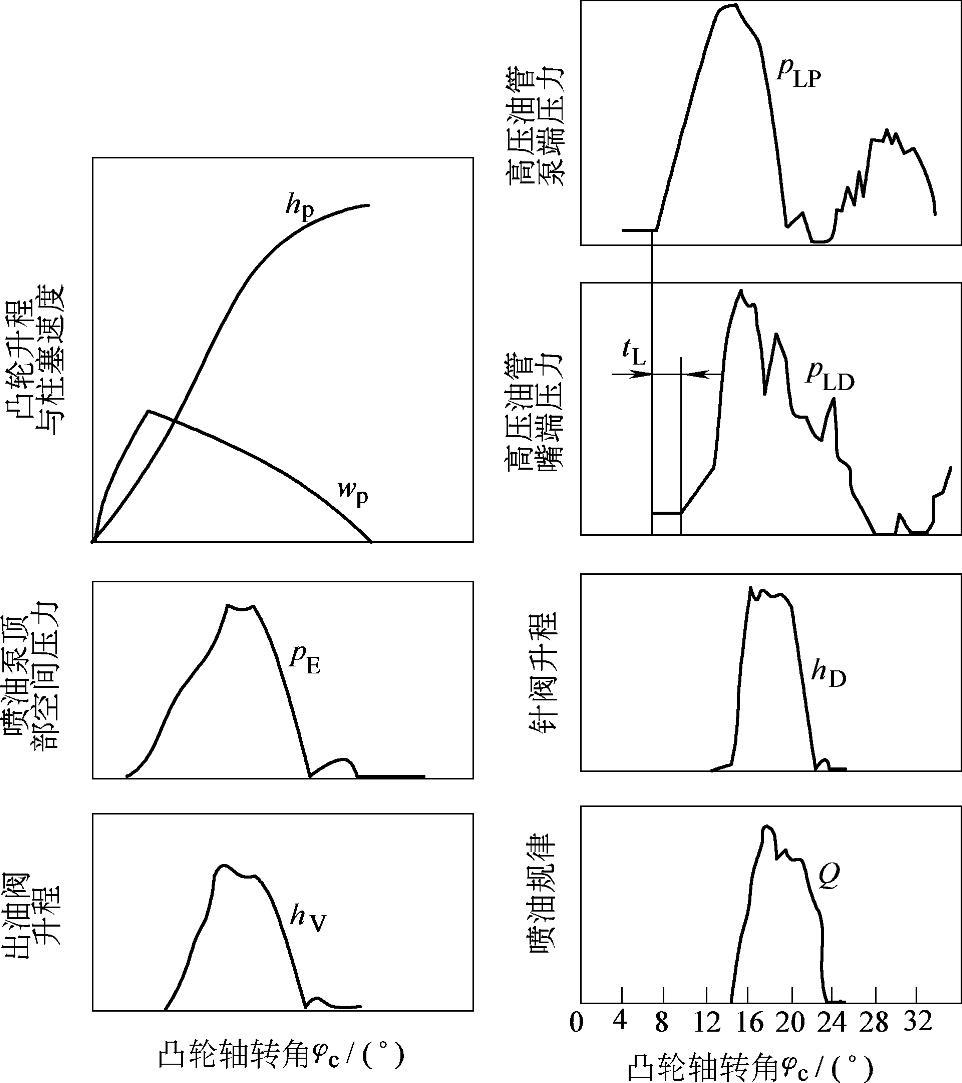
图3-11 典型燃料供给系统的计算结果

h_p—凸轮升程 w_p—柱塞速度 p_E—喷油泵柱塞顶部空间压力 h_V—出油阀升程 p_LP—高压油管泵端压力 p_LD—高压油管嘴端压力 h_D—针阀升程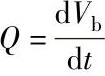—喷油规律

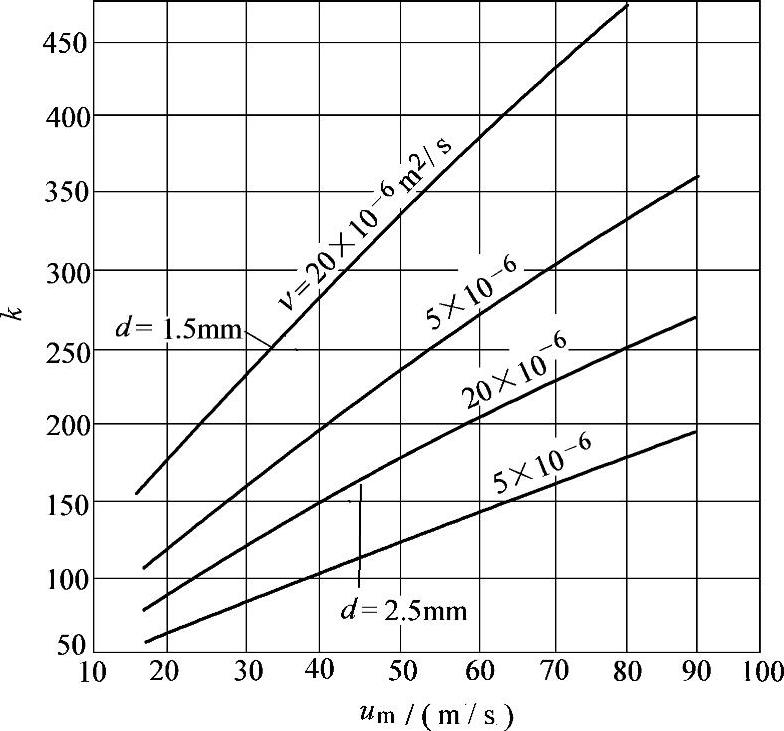
图3-12 高压油管内径d、燃油粘度ν以及燃油平均流速u_m与流体阻力系数k之间的关系

实际上，波动方程是可以通过特征线法将其化为常微分方程来求解的，而图3-10的x-t平面中斜率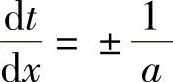的交叉线簇即为压力波传播的特征线。

总之，对于整个喷油系统，若能建立从喷油泵经高压油管至喷油嘴各个环节的物理与数学模型且能弄清楚各环节之间的相互联系，即不难采用数值计算方法在计算机上联立求解，得出泵端压力、喷端压力、针阀升程与喷油规律在内的各种重要参数（图3-11），从而使我们对整个燃料供给系统的工作有一个全面的了解，以便研究各参数变化对整个系统工作的影响。

但是为了使计算工作不要过于复杂，在一般计算中往往也作出很多简化与假设，例如：

（1）不考虑管壁摩擦带来的流动损失，这一点对于管道不太长（不超过1m）的情况，不会引起很大的误差，对于管道较长的情况，则需考虑因流体阻力而引起的压力损失，为此引入了摩擦阻力项：

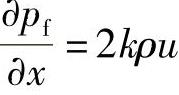
式中，k表示流体阻力系数，其值取决于高压油管的内径、壁面粗糙度以及燃油的流速与粘度（图3-12）。

这样，式（3-30）就变为

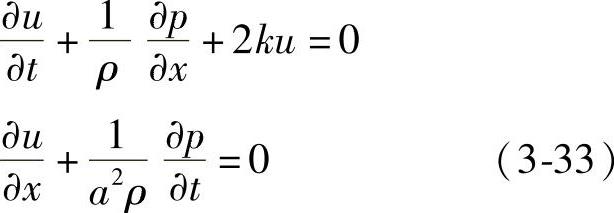
相应的波动方程则变为

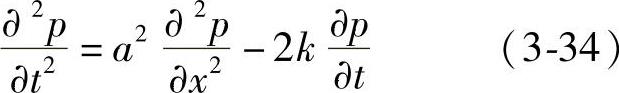
或

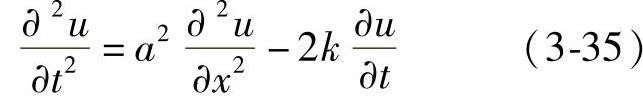
其解为（推导从略）

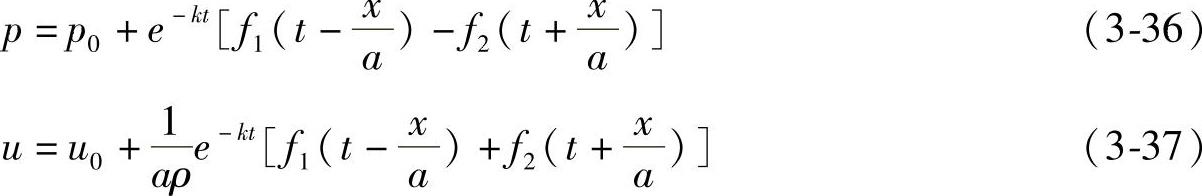
对比式（3-31）、式（3-32）与式（3-36）、式（3-37）可知，当有管道摩擦阻力存在时，压力波与速度波是随时间逐渐衰减的。

（2）不考虑燃油温度的变化。这一点对于喷油压力不高的情况，不致引起很大的误差，但是随着喷油压力的提高与压力变化的加剧，燃油温度的变化就不得不予以考虑，因为当压力变化10MPa时，燃油温度变化约为1.2K，而燃油温度的变化反过来又会对其粘度与密度产生影响，从而影响喷油过程。为了计算燃油的温度，除了压力变化以外，还必须考虑管壁传热以及壁面摩擦与局部节流损失等引起的能量耗散，为此必须引用热力学第一定律与传热学方面的知识。

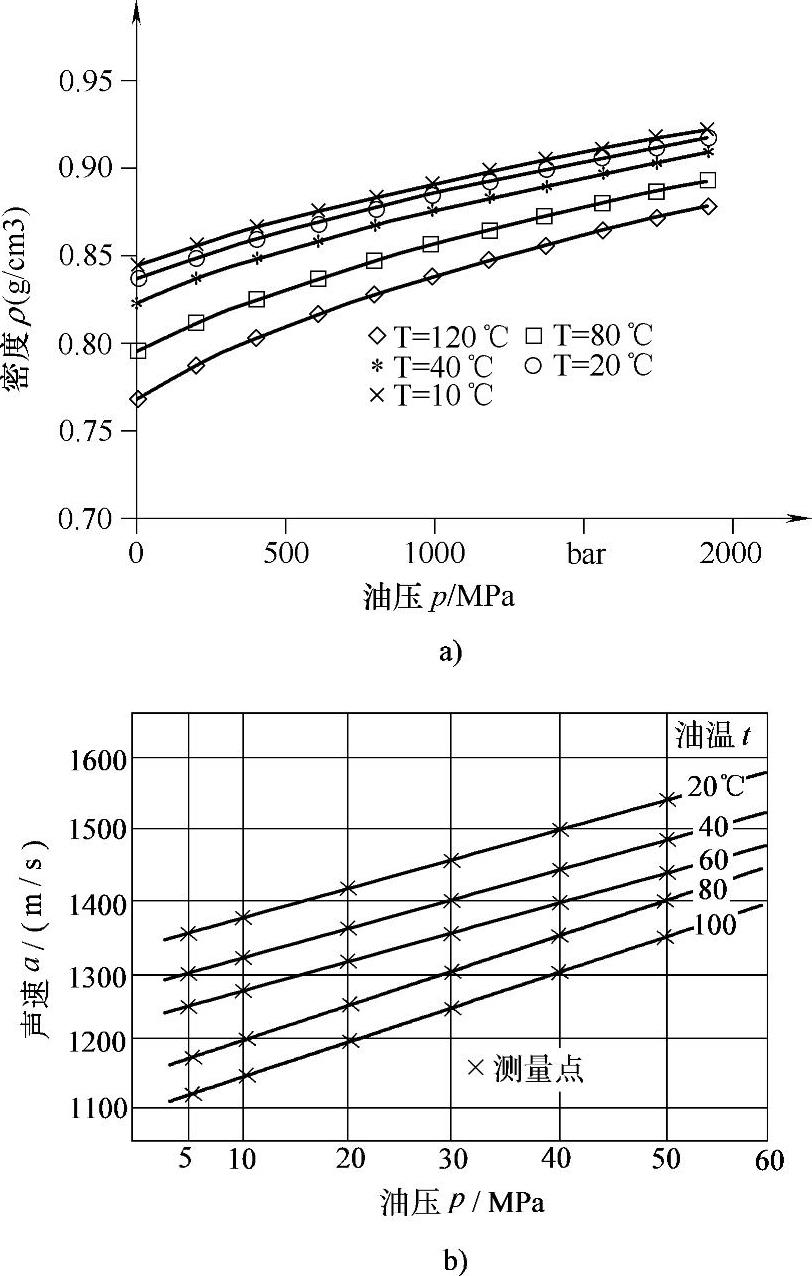
图3-13 轻柴油密度与声速随压力与温度的变化关系

a）密度的变化b）声速的变化

（3）将燃油密度与弹性模量（即声速）以及粘度均视为常数。这一点在燃油压力不高的情况下也不致引起很大误差，但是在高压喷射系统（泵-喷嘴与共轨系统）计算时，则不能不予以考虑，例如在图3-13中，图a表示燃油密度随压力与温度的变化关系，图b表示在高压无“气穴”现象时，燃油中声速随压力与温度的变化关系。

（4）对喷油系统内的气穴（Cavitation）现象，只作以简单的处理，即认为压力等于零时产生气穴，然后用质量守恒定律（连续方程）计算气穴容积的形成或填充。应当指出，用这种简单处理的方法很难得到满意的计算结果。因为气穴产生时，破坏了介质的连续性与压力波传播的规律。这时比较合理的方法，是将产生气穴以后的燃料作为两相介质处理，采用较低的声速进行计算，才能取得较为精确的计算结果。两相介质的声速除了与压力p、温度T和密度ρ有关以外，还受到空隙率α=ΔV/V（V为系统总容积，ΔV为其中的气穴容积）的很大影响，其表达式为

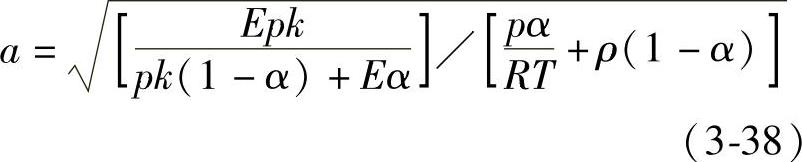
式中，除a为声速（m/s）以外，还有E为燃油的弹性模量（MPa），ρ为燃油的密度（kg/m³），R为空气的气体常数[可取287.04J/（kg·m）]，k为空气的绝热指数（可取k=1.4），T为两相介质的温度（K）。

如图3-14所示为各种压力状态下柴油-空气两相介质的声速a随空隙率α的变化关系。

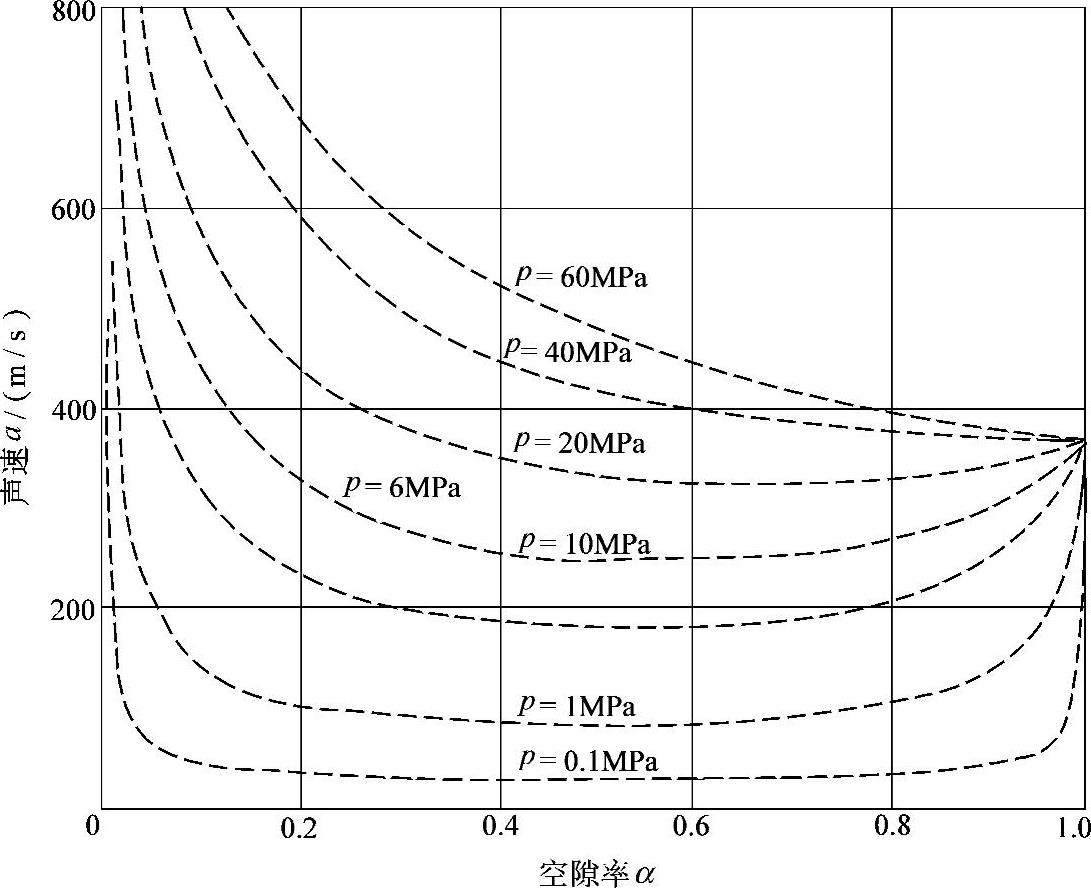
图3-14 各种压力状态下柴油—空气两相介质的 声速a随空隙率α的变化关系

图3-15所示为在一台采用等容式出油阀泵-管-嘴的单缸试验机上，测得的实际声速随V_E/V_S比值（V_E为出油阀卸载容积，V_S为系统高压部分总容积）的变化关系。

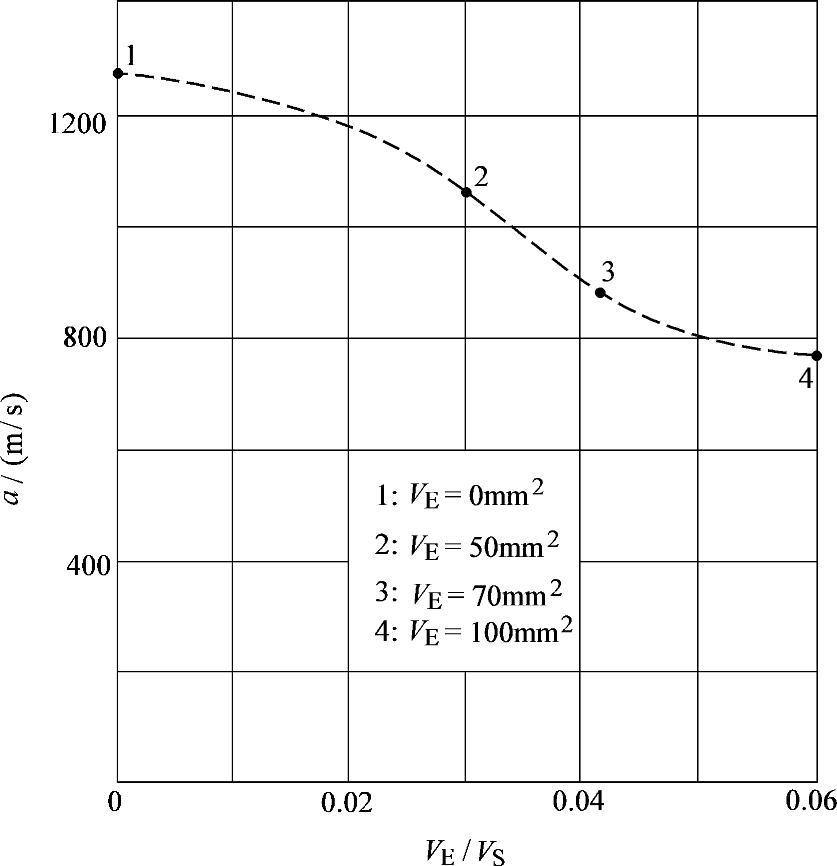
图3-15 柴油机高压油管内实测声速随比值V_E/V_S的变化关系

（5）不考虑精密偶件的泄漏与承受高压零件的弹性变形等。这一点也只能用于喷油压力不高的燃料供给系统中，对于现代高压喷射系统，上述因素也是不应回避的，例如通过精密偶件配合间隙的泄漏量可用以下半经验公式计算：

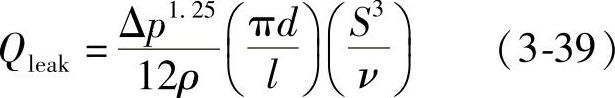
式中，Δp为泄漏处两端的压力差，ρ为燃油密度，πd为环形间隙的周长，l为密封长度，S为半径方向的配合间隙，ν为燃油的运动粘度。由此可以看出，当压差Δp与密封件几何尺寸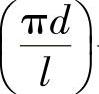一定时，泄漏量正比于间隙的三次方，反比于燃油的粘度，而粘度又随燃油的温度与压力而变（温度与压力对粘度影响正好相反，粘度随温度增加而降低，随压力增加而增加，但温度的影响更为明显），有关这方面的资料可查阅专门的文献。由此可见，在高压燃料供给系统的计算中，考虑配合间隙的泄漏量时，不应当忽视高压作用下零件变形以及温度与压力变化对燃油粘度的影响。

正是由于存在以上简化与假定，再加上计算中还存在一些必须由实验确定的参数，因此有时使我们难于得到真实反映实际喷油过程的计算结果。为此在建立计算程序时，应尽可能对那些难以用计算确定的数据采用部分试验结果（如在专用的流量系数试验台上测量喷孔或其他流动截面的μf值，在高压油管中根据压力波传播时间测定实际声速，等等）。同时，也启发了我们开发一些基于试验结果来计算喷油过程的更为简便与快捷的计算方法，例如可以根据实测油管压力来计算喷油过程，这时如果测点选得尽可能靠近喷油嘴，并充分考虑喷油器内的结构细节，将有助于节约计算工作量（无需从泵端开始计算），并能大大提高计算精度。

总之，随着对燃料供给系统研究的深入与计算机容量与运算速度的提高，计算方法也在不断完善。特别是在喷油压力不断提高的情况下（高压泵-管-嘴系统、泵-喷嘴系统与共轨系统），更应对影响其喷油过程的各项因素作更为细致周到的考虑，才能取得满意的计算结果。