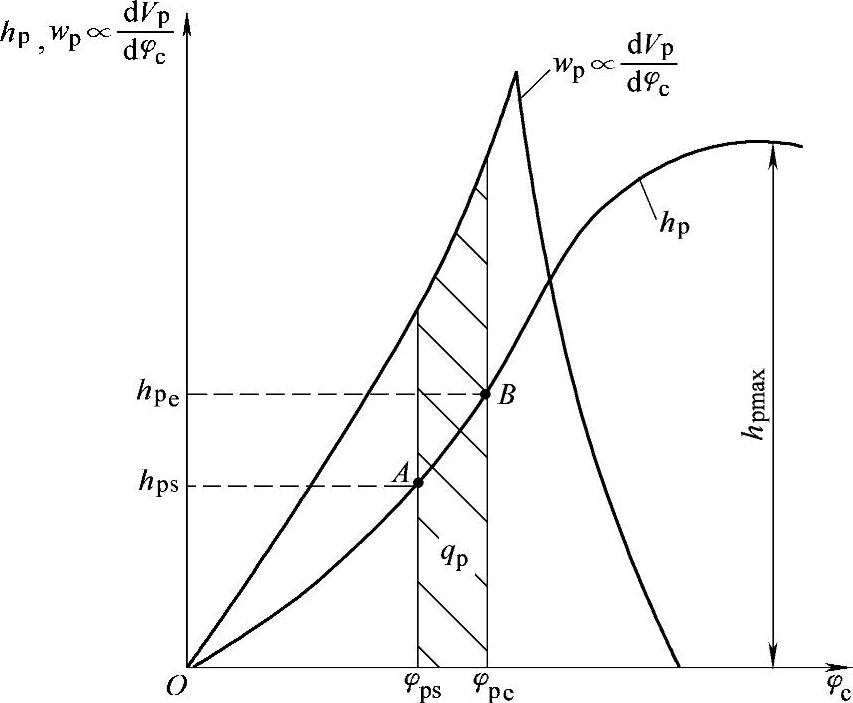
图3-3 柱塞升程及供油率曲线

几何供油规律，或简称供油规律是指从几何关系上求出的单位凸轮转角（或单位时间）内喷油泵供入高压油路中的燃油量即供油率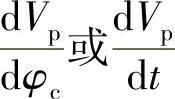随凸轮转角φ_c（或时间t）的变化关系（供油率有时也称供油速率）。它完全是由柱塞的直径和凸轮型线的运动特性决定的，即

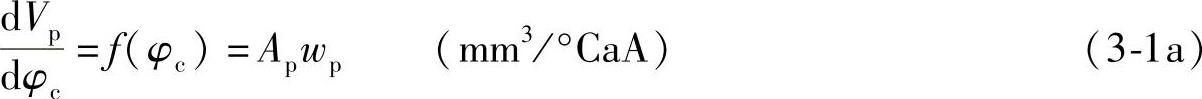
或

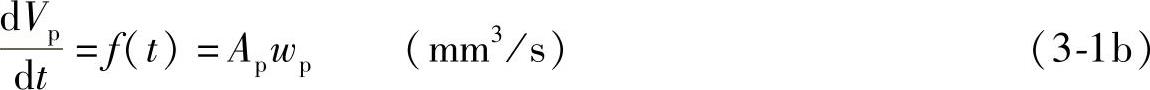
式中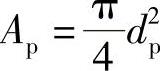，为柱塞顶面积（mm²），d_p为柱塞直径（mm），w_p为有效行程段的柱塞速度，在式（3-1）中w_p的单位按凸轮转角计，即mm/℃aA，式（3-1a）中w_p的单位为mm/s。

在图3-3中，曲线h_p为挺柱升程，w_p为挺柱或柱塞速度，当柱塞顶面积一定时，w_p正比于几何供油规律，即w_p∝^dVp，h_ps

dφ_c相当于几何供油始点（柱塞顶面关闭进回油孔），h_pe相当于几何供油终点（柱塞螺旋槽或斜槽棱边打开进回孔），（h_pe-h_ps）=h_e为几何有效供油行程，柴油机运转时，由于进回油孔的节流作用，实际供油量会略大于几何供油量，即柱塞的实际有效供油行程会略大于几何供油行程，φ_pe-φ_ps=Δφ_p为几何供油持续角，图上的阴影线面积乘以柱塞面积A_p后即为每循环几何供油量q_p，即

q_p再除以几何供油持续角Δφ_p后即可得平均几何供油率，即

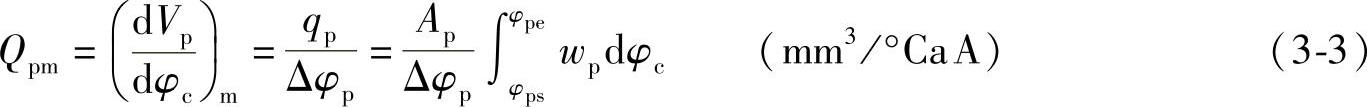
以上供油规律及其相关参数如q_p和Q_pm等既是设计喷油泵的主要依据，也是评价喷油泵工作能力的重要指标。

喷油规律是指在喷油过程中，单位凸轮转角（或单位时间）内从喷油器喷入气缸的燃油量，即喷油率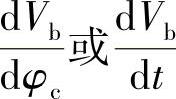随凸轮转角φ_c（或时间t）的变化关系（喷油率有时也称喷油速率），即(www.daowen.com)

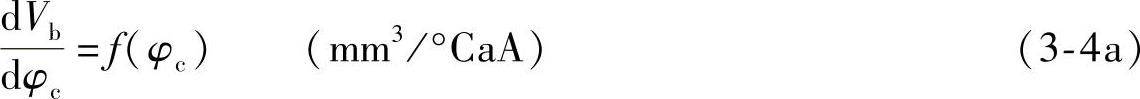
或

喷油规律的表达式与供油规律相似，而且它也是由供油规律演变而来的，但由于整个系统综合作用，因此在形状与相位上均与供油规律有明显差异（图3-4）。

由图可见，首先由于高压油管的压力波从泵端传到嘴端需要一定的时间，喷油规律的始点B（φ_js）要迟于供油规律的始点A（φ_ps），即存在一个喷油滞后角Δφ_pj。其次，由于高压油路中燃油的可压缩性等因素的影响，喷油的持续时间要大于供油持续时间，即Δφ_j>Δφ_p，喷油规律曲线的峰值也就相应小于供油规律的峰值。再考虑到燃油在高压下通过柱塞精密偶件微小缝隙的泄漏，则喷油规律曲线面积下表示的每循环喷油量q和平均喷油率Q_m，即

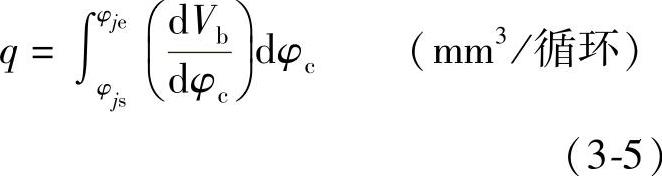
和

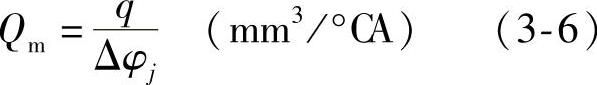
均要略低于每循环几何供油量q_p和平均几何供油率Q_pm。最后，喷油规律的曲线形状也与供油规律有明显的不同。

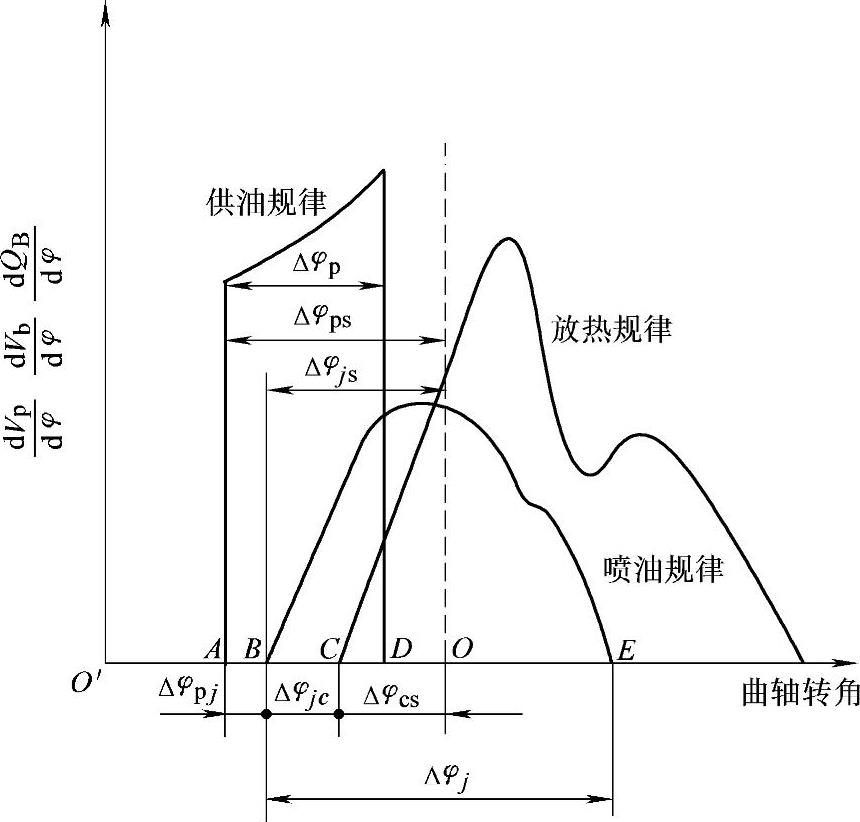
图3-4 几何供油规律、喷油规律与放热规律之间的比较

A—几何供油始点（φ_ps） B—喷油始点（φ_js） C—燃烧始点（φ_cs） D—几何供油终点（φ_pe） E—喷油终点（φ_je） O—上止点 Δφ_ps—供油提前角 Δφ_p—供油持续角 Δφ_js—喷油提前角 Δφ_pj—喷油滞后角 Δφ_j—喷油持续角 Δφ_cs—着火提前角 Δφ_jc—着火滞后角

在前一章中已说明，喷油规律对柴油机的燃烧过程有着重大影响，为此，在图3-4中也给出了柴油机燃烧时的放热规律曲线，它也是在喷油规律的基础上通过混合气形成与燃烧而形成的。通过对图中供油规律、喷油规律与放热规律三条曲线的比较不仅可以使我们看到三者的区别，也有助于我们进一步理解三者之间的因果关系与内在联系，需要说明的是，为了便于和放热规律比较并正确定义相互之间的各种角度，图3-4中的供油规律与喷油规律曲线上的纵坐标均已转换为单位曲轴转角的供油率或喷油率，横坐标则为曲轴转角。