在柴油机中采用高压喷射的目的主要是使燃油雾化，以形成细小的油滴群，这样就可以大大增加燃油的蒸发的面积，从而加速热空气与燃油液滴之间的传热过程，并增加其与氧气接触的机会，保证油滴在极短的时间内迅速蒸发并与空气形成可燃混合气。例如，把直径0.3mm的油滴雾化为直径3μm的油滴，其数目将达一百万颗之多，它们与空气接触的面积比原来增加了1万倍，由于燃料质量燃烧率大致正比于油滴总面积，则燃烧速率也可以增加大约1万倍。由此可见，对于燃油雾化（Atomization）和油束或喷注（Spray）特性进行深入研究是改善柴油机燃烧特性与排放特性的关键。但遗憾的是，由于这一问题的复杂性，尽管人们已为此倾注了很大的精力，但对其中许多问题仍然认识不清，其原因是柴油机的燃油喷雾是一个复杂的动态过程，它系在高压下，通过喷嘴上细小的喷孔将燃油喷入压力与温度均不断变化的燃烧室中来实现的，其间伴随着油滴破裂、相互碰撞与聚合、油滴蒸发、油束碰壁等多种复杂现象，因此它不仅取决于喷油压力和喷嘴结构与尺寸，而且还受到燃油性质以及气缸内压力、温度与气流运动等多种影响因素的影响。而我们目前对其中许多现象的机理还缺乏满意的解释。因此，本书只能从工程技术应用的观点，对燃油雾化与油束形成的过程及其若干评价指标作一简单描述。

一般认为，燃油喷入燃烧室后，喷注在高速前进过程中，其前锋与周边均遇到相当稠密的热空气阻力（包括摩擦力与形状阻力），同时液体本身具有很大的扰动，致使飞驰中的液注不断被撕裂、破碎与雾化。已形成的较大颗粒的油滴，又由于韦伯效应而不断细化为更小粒径的油滴，形成直径为2～30μm的雾状油滴群并进一步蒸发与形成可燃混合气。

韦伯（Weber）效应的机理是，任何液滴在运动过程中，如果其惯性力超过其表面张力一定倍数后，则该液滴将被分裂为更细的液滴，它反应的是空气动力效应对雾化的影响，即液滴的动能对于燃油雾化所需能量的贡献。为此，人们把液滴运动惯性力与表面张力之比称为韦伯数We。

式中ρ_f——燃油的密度，对于柴油为820～845kg/m³；

σ——油滴的表面张力，对于柴油为21～31N/m；

d_j——油滴直径（m）；

v_j——油滴前进速度（m/s）。

试验证明，单个油滴的破碎条件为，We≥12，将这个条件代入式（2-75），并取燃油的ρ_f=845kg/m³和σ=30N/m得

或

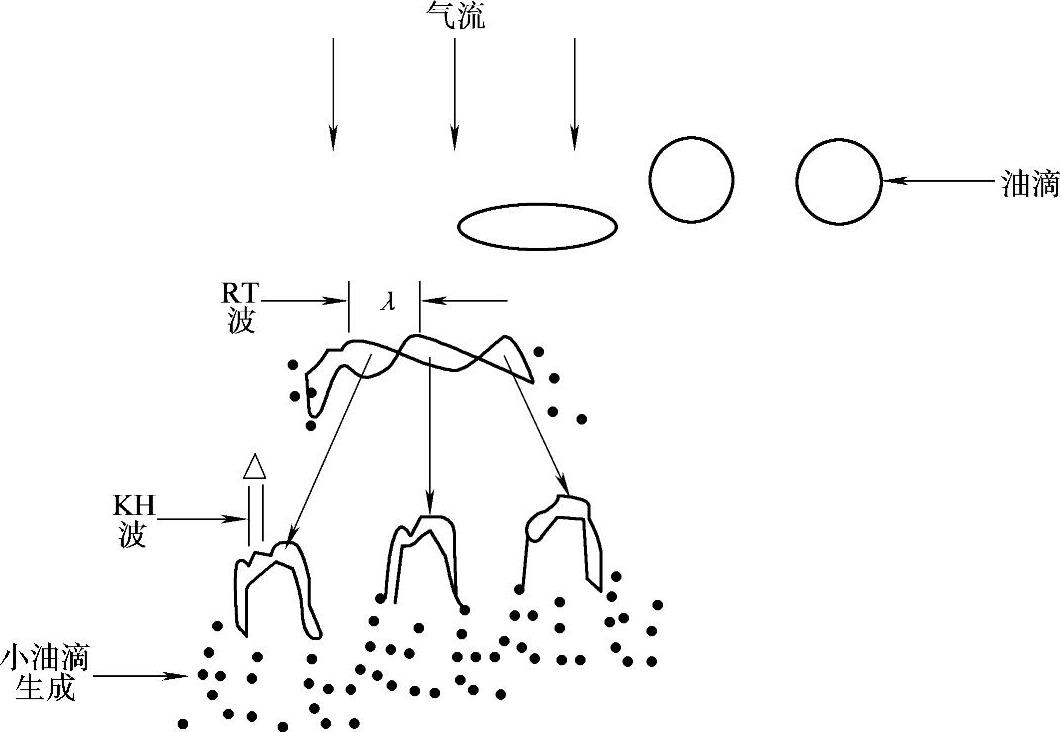
图2-34 高速油滴破碎机理的示意图

若取喷嘴出口处的油滴直径等于喷孔直径，假定为0.2mm=0.2×10^-3m，则可按式（2-76）算得使该油滴破碎的最低速度为46.6m/s，实际上由于目前柴油机广泛采用高压喷射，当喷油压力达到80～100MPa，喷孔直径又相当小时，喷孔处的流速高达200～300m/s，韦伯数We亦大于100，因而能保证良好的雾化条件。按式（2-77），当v_j=200m/s时，d_j可小于5μm左右。当然，以上分析还是十分粗略的，实际上油滴的破碎过程受到多种力的作用，不仅有外力的作用，也受到喷柱内部扰动的影响，机理十分复杂，早期泰勒（Taylor）曾用研究质点振动的方法类比油滴的破碎问题，称为泰勒类比破碎模型（Taylor′s Analogy Breakup Model）简称为TAB模型，它套用了单质点的振动方式求解，设油滴直径为d_j，在各种外力作用下发生振动，若振幅x大于d_j，则认为油滴破碎，但这种方法考虑的因素较单纯，只适用于低速运动的油滴。此后，美国威斯康辛大学（University of Wisconsin-Madison）的研究学者又根据高速液体射流（jet）与液滴运动的研究，建立了Kelvin-Helmoltz（KH）波动模型和Rayleigh-Taylor（RT）波动模型，并将其写入著名的KIVA程序，以替代原有的TAB模型，从而提出了比较适合于柴油机喷油过程高速运动油滴的破碎机理，其原理如图2-34所示。图中，球形油滴在高速气流的作用下变成扁平形，然后在Rayleigh-Taylor（RT）不稳定表面波作用下，加速油滴扁平化，并分裂出一些大尺度碎片，然后在更短波长的Kelvin-Helmo-ltz（KH）不稳定表面波作用下，把大尺度碎片割成丝状，然后生成更细的油滴，而油滴群的集合体，即为油束，或称喷注。

然而，直至20世纪90年代为止，几乎所有的喷雾与燃烧模型，均是根据假定的边界条件（如出口流速等）认为在喷孔出口处已形成了同样尺寸的油滴或是油团（blob），由此计算它们在燃烧室中前进过程的破碎情况，而忽略了喷油过程与喷孔中燃油流动的影响，这就出现了从喷油过程到燃烧过程计算中的脱节情况。

近年来，德国汉诺威（Hannover）大学的梅克尔（Merker）等人为了弥补了这个空缺，提出了喷雾两阶段理念和相应的数学模型，即将燃油雾化分为初次雾化与后续雾化两个阶段。其机理如图2-35所示。

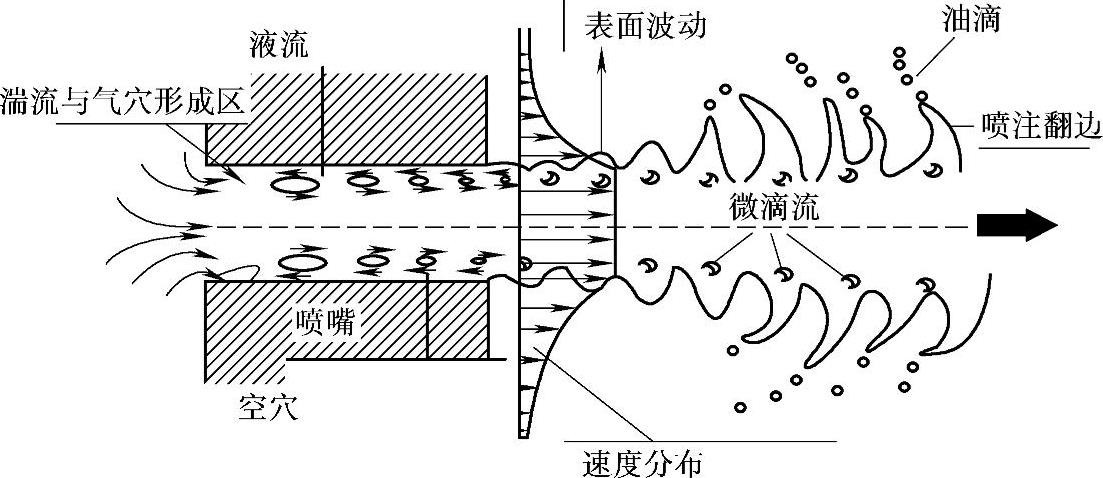
图2-35 燃油在喷孔内及喷孔附近的雾化情况

图中的第一阶段，即初始雾化阶段发生在喷孔内及前方距喷孔直径不到5～10倍的距离处，这时由于燃油在喷孔入口处的急剧转向以及在喷孔内的高速流动，产生的湍流（Turbu-lence）和气穴（Cavitation，又称空穴）效应会促使燃油的分裂，有助于油滴的形成。液柱中的湍流或微涡流引起的扰动，能为油滴破碎提供所需的能量是不言而喻的，而由于液流内局部真空形成的气穴（包括从溶解在燃油中空气析出的气泡或由于压力低于饱和蒸汽压时而产生的燃油蒸汽泡）一旦从喷孔进入燃烧室溃灭时产生的能量，同样也能促进燃油的雾化。由于气穴的形成条件与喷油嘴的结构和尺寸、燃油的喷射压力、温度以及挥发性质密切相关，因此这一阶段的喷雾情况也受到上述因素的很大的影响。第二阶段，即后续雾化阶段，则是油滴在燃烧室的行进过程中进行的，主要受气体阻力，即前述韦伯效应的影响。对于这一阶段的研究已比较充分，有关数学模型（如威斯康辛大学的RT-KH波模型）也比较成熟。现在，汉诺威大学主要针对初始雾化阶段，将计算喷孔内液体流动的欧拉（Euler）方程与计算空间雾化的拉格朗日（Lagrange）方程相结合，在两相流理论和气泡动力学基础上，建立了这一中间阶段的数学模型并将其植入CFD-Code KIVA3V程序中，从而构成喷油至燃烧过程完整计算链。由此可见，只要人们能在充分考虑喷油与燃烧系统结构细节的基础上，对喷油过程、油滴雾化、蒸发混合气形成与燃烧各个环节及其相互关系进行深入研究，即不仅能根据喷油规律计算出放热规律，而且能够对于柴油机的整个燃烧过程及其动力、经济与环保性能作出更为精确的预测，尽管这项工作目前尚不完善，但却为内燃机科技工作者指出了一个重要的努力的方向。

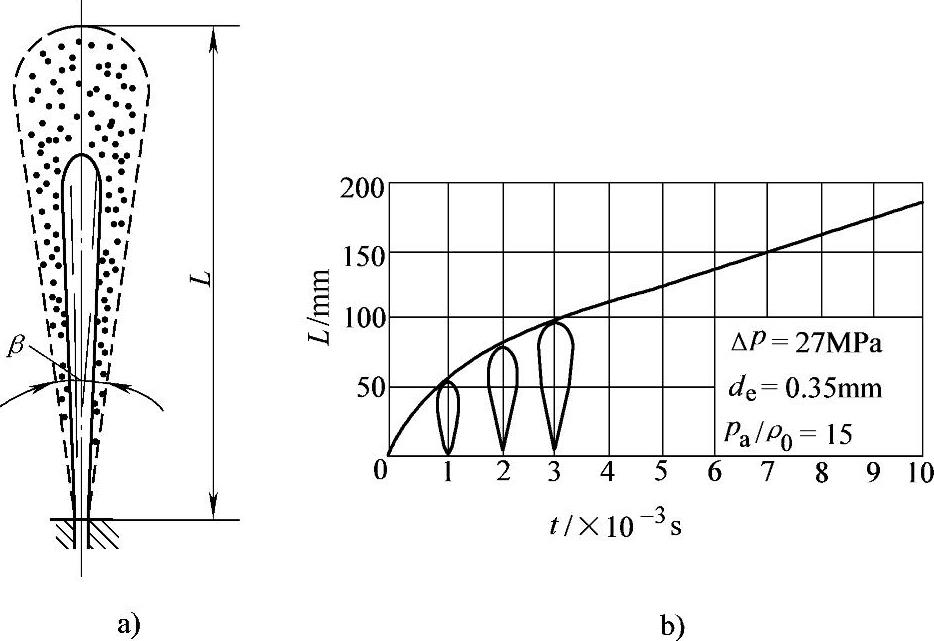
图2-36 油束及其射程随时间变化的关系

a）油束简图 b）射程随时间变化关系

最后还要简要介绍影响燃油在燃烧室内宏观与微观分布的几个评价参数，它们是：

1.油束射程

如图2-36a所示为油束的简图，油束射程（Spray Penetration）或称油束的贯穿度表示油束的前锋至喷孔出口处的距离L，它对于燃油在燃烧室的纵深分布具有重要意义，选择合适的油束射程有助于提高燃烧室中空气的利用率，从而改善混合气的形成与燃烧。对于小缸径柴油机，因其燃烧室尺寸较小，必然会有一部分燃油喷射在温度较低的壁面上，增加了HC和CO的排放，当燃油从壁面反射时，若与相邻油束重叠过多，又会因局部缺氧，造成碳烟与微粒排放增加。反之，对于缸径较大的柴油机，若油束射程不足，也会使燃油得不到足够的空气而使柴油机的燃烧与排放性能恶化。因此，油束的射程必须根据具体机型及其混合气形成特点与燃烧室很好的配合。

在实际柴油机中，由于油束形成时伴随着复杂的燃油雾化、蒸发与燃烧过程，其射程随时间不断变化，因此很难精确测定，但是作为初步估算，则有不少经验与半经验公式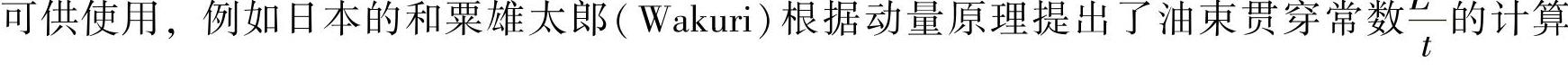

式中L——油束射程（m）；

t——贯穿时间（s）；

d_c——喷孔直径（m）；(www.daowen.com)

β——喷雾锥角；

μ_c——喷孔流量系数；

Δp——喷孔处压力差（Pa）；

ρ_a——缸内空气密度（kg/m³）。

当柴油机运行工况一定时，压缩比ε与充量系数_ηv一定，则ρ_a大致不变，燃料供给系统确定后，喷孔直径d_c与喷油压力一定，则Δp、μ_c、β等也大致不变，据

L²此=常数（因此称为贯穿常数），L∝

t t，即油束射程随时间t大致呈如图2_-36b所示的抛物线关系变化。式（2-78）的另一个形式为

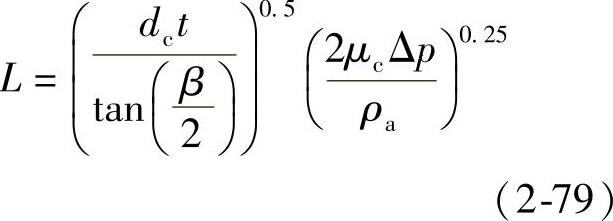
假定油束锥角β=16°，喷孔流量系数μ_c=0.7，则式（2-79）可简化为

式中各项的单位与式（2-78）相同。

包括和粟公式在内的许多计算公式，均因其理论上的假定和试验依据与实际情况有一定差别，而不可能十分准确，而且它们主要适用于油束碰壁以前的情况，对于缸径较小的直喷式柴油机还应考虑燃油碰壁时撞击、转向和反弹等许多复杂的现象，这方面问题虽已有专门文献介绍，但还需进一步深入研究。

2.喷雾锥角

喷雾锥角又称油束夹角，在图2-36a中用β表示，它在油束的前进过程中也是不断变化的。喷雾锥角说明油束的紧密程度，β大表示油束比较松散，油束射程短（参见式2-78或式2-79），β小表示油束紧密，油束射程较长。由此可见，它对燃油在燃烧室的分布也有重要参考价值。喷雾锥角的大小主要受喷油压力与喷孔尺寸的影响，作为初步估算，同样也有很多经验公式可供使用。例如，广安博之（Hiroyasu）和新井雅隆（Arai）根据容弹试验和量纲分析提出的公式为

式中，ν_a为缸内空气的运动粘度，单位为m²/s，其余Δp、d_c、ρ_a的意义与单位与式（2-78）相同。

3.雾化质量

雾化质量又称雾化特性，表示燃油喷散雾化的程度，一般是指喷散的细度和喷散的均匀度，喷散得越细，越均匀，说明雾化质量越好。由于燃油的喷雾中的油滴大小不同，因此只能用其平均值来表示。表示油粒平均直径的方法很多，其中应用最广的是绍特平均直径（Sauter Mean Diameter，简写S.M.D.），其定义为

式中N_i——直径为d_i的被测量的油滴数量；

K——直径分档数。

S.M.D的物理意义是全部油滴的体积与其总面积之比，反过来，假定全部油滴的直径等于S.M.D时，其总体积与表面积将保持不变，这样就能保持油滴受热与蒸发的条件大体不变。影响油滴雾化的因素很多，根据棚择泰（Tanasawa）和丰田（Toyota）的实验，它与喷孔直径d_c，油束在喷孔出口处流速v_j、燃油的粘度ν、燃烧室内空气的密度ρ_g和燃油的密度ρ_f等一系列因素有关。

英国里卡多（Ricardo）公司则抓住其中主要影响因素（喷孔直径d_c和影响喷孔内燃油流速的压差Δp），在假定燃油温度为573K的条件下，给出了适于工程上应用的简化公式，即

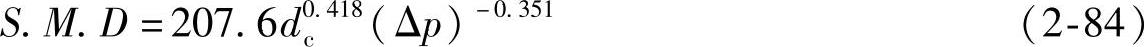
式中，d_c单位为mm，Δp单位为bar，求出的S.M.D.单位为μm。由此可见，喷油压力越高，喷孔越小则S.M.D.也越小。

前已说明，绍特平均直径主要用来说明燃油雾化的细微度，S.M.D.越小，喷雾越细，但是并不能反映喷雾的均匀度，后者可用油滴最大直径与平均直径之差来表示，这个差值越小，喷雾越均匀。另外，也可以用实验的方法，把油束中的油滴直径测量出来后，画成曲线来表示油粒的细度和均匀度，这种曲线称为雾化特性曲线，如图2-37所示，横坐标是油滴的直径，纵坐标是某一直径油滴约占全部油滴的百分率。曲线越窄，越靠近纵坐标轴，表示油滴越细越均匀，即雾化质量越好。

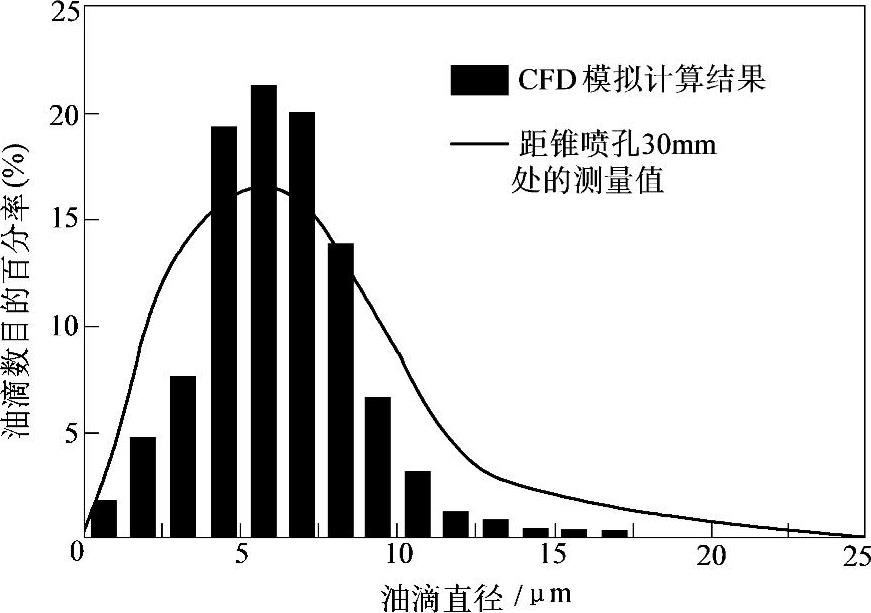
图2-37 雾化特性曲线