在上节中，我们提到了系统故障的问题，当存在执行器故障的情况下ud=umax，事实上这样对于实际控制是很不利的，在该种情况下，在饱和状态消失之前，所设计的右互质分解控制器将不能发挥作用，闭环控制系统敏感性大大降低，严重情况下可以使系统性能严重恶化，不论是理论研究还是实际应用都会带来相当大的影响。针对这种情况，在状态饱和部分，我们运用滑模变结构控制的原理对饱和部分进行处理，将滑模变结构控制与演算子理论的鲁棒右互质分解方法结合起来对液位控制系统进行理论研究，并将研究结果应用于实时控制中，系统性能得到了明显的改善。

7.5.1　故障系统的滑模变结构控制

滑模变结构控制器的设计目标一是理想的滑动模态，二是良好的动态品质，三是较高的鲁棒性。因此，滑模变结构的设计主要分为两方面，一方面是滑模面的选择，使系统能够具有较好的趋近率，能够稳定在滑模面上下运动，使系统保持渐进稳定；另一方面是控制率的选取，使系统能够在一定时间内运动到滑模面，且具有较好的运动性能。

滑模变结构设计中滑模面的选取由发展初期的线性滑模面到非线性滑模面和时变滑模面，滑模面的设计发展使滑模控制具有了更好的控制性能，如非线性滑模面中引入非线性函数，使得系统的收敛时间取得了很大的提高。对于一个存在滑动模态的控制系统，当切换函数的趋近率趋近于零时，该函数的积分也将趋近于零，因此，在滑模面的选取中出现了积分形式的滑模面，如在线性滑模面中增加积分环节后，可以削弱系统的抖振、具有减小稳态误差的功能。积分滑模面的选取可以让我们很好的对非线性系统进行控制，保证了系统的稳定性能，不过该控制也存在着一定的缺陷，当初始状态比较大时，积分环节的引入可能会引起系统造成很大的超调或者给系统执行机构带来饱和状态。

滑模变结构控制中控制率的选取要能够保证系统的可达性，即系统从空间的任一状态都能在有限时间到达滑模面，并具有渐进稳定的性能，通常选取的控制结构形式有以下所述三种形式：

（1）常值切换函数：

式中：u0为带求常数。

（2）函数切换控制：

这种控制结构形式是建立在等效控制基础上的。

（3）比例切换控制：

式中：αi，βi为常数。

对于这些切换控制中，通常第二种方法用得比较多，重要的是根据系统的特定性能选取相对应的方法。本课题主要采取切换控制的方法去实现控制目的。

滑模变结构控制的运动品质分别有运动段和滑模段决定，正常运动段的趋近过程要求运动良好，满足稳定性，这里采用具有趋近率的方法完善该运动品质。四种常见的趋近率如下：

（1）等速趋近率：

（2）指数趋近率：

（3）幂次趋近率：

（4）一般趋近率：

选取原则为根据系统的特定性能保证该系统状态点离开选择的切换面时能够使其以较快的速度趋近切换面，但同时要注意趋近速度过大可能会引起系统抖振加剧，所以要合理选择，使系统满足综合性能指标。

对于公式（6-5）所建立的水箱液位模型，我们对其进行滑模变结构控制的方法对其进行控制器的设计。针对该系统，首先需要将其转换为状态方程形式，我们取状态变量为：(www.daowen.com)

式中：e为设定液位与实际液位之间的偏差值；r0为设定值；y（t）为实时采集液位值。得到状态方程为：

对于该状态方程，我们选取滑模面切换函数s（x）为：

即：

从上述公式我们可以看出，当状态点运动到滑模面后，上式收敛，且仅与参数c有关，与对象参数无关，验证了其鲁棒性[22]。

为了得到控制率u，使系统以较短的时间到达滑模面，我们采用指数趋近率如下：

对该控制率进行稳定性分析得到如下公式：

由于ε＞0，k＞0，所以我们得到满足滑模变结构控制的可达性条件，成功证明该系统能够稳定在该滑模面上，当在滑模面上运动时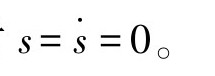

由上述滑模面切换函数和指数趋近率，根据公式（7-32）我们可以得到：

由此解得控制率为：

对于该具有饱和状态的鲁棒非线性控制系统，在设计控制器处理饱和状态时，我们将鲁棒右互质分解的方法与滑模变结构的方法结合起来，滑模变结构将饱和部分转化一个切换面，克服了饱和现象。而鲁棒右互质分解方法保证了系统的鲁棒稳定性，能够使系统在较好的状态下运行，由以上条件控制器设计为：

式中：

7.5.2　仿真与实验结果分析

首先对上面提出的方法所设计的控制算法进行系统仿真，仿真如图7-25所示，其中B=0.01，C=0.0004，ε=0.099，k=0.2，r0=30cm。仿真结果显示，设计的控制器很好的处理了状态饱和部分，该控制器对于输入受限的处理起到了较好的效果，该控制器可以用于实际控制实验中。

图7-25　设计控制器仿真图

将设计的控制器在实验平台上运行，液位和执行机构的输入采集图如图7-26所示，该控制器具有鲁棒稳定性，系统超调低于5%，稳定时间大约为400s，图7-27为PID控制系统图，超调量为6%，在600s时达到稳定，稳定时间较长，两者相比，设计算法响应时间较快，超调量较小，具有较好的动态特性，设计控制器调节阀输入部分放大图如图7-28所示，在系统刚开始运行的阶段，控制器并没有达到饱和，大大提高了控制器的灵敏度，控制效果良好，实验结果验证了设计的有效性。

图7-26　提出的控制算法实验图

图7-27　PID控制过程图

图7-28　输入部分放大图