首先，对建立好的模型进行鲁棒右互质分解，使其满足鲁棒稳定性，设计跟踪算子使之达到跟踪性能。对于系统P，如果存在两个因果稳定的算子N：W→Y,D：W→U,D在U上可逆，并且使得P=ND-1或PD=N那么称P存在右分解。如果P存在右分解P=ND-1，且存在因果稳定的映射S：Y→U,R：U→U使如下Bezout恒等式成立：SN+RD=IU或（R　S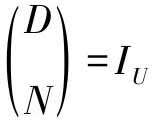），则称P存在右互质分解，其中IU为U上的单位映射。如果P存在有界扰动ΔP，带扰动的系统依然存在右互质分解性，则称系统存在鲁棒右互质分解[4～11]，如图7-1所示。

图7-1　鲁棒右互质分解

根据以上定理，珀尔帖装置模型可以进行右分解：

所设计的右互质分解控制算子R与S为：

为了检测故障信号，设计三个算子R0、S0和D，如图7-2所示，使之满足以下Bezout等式[13～26]：(www.daowen.com)

由此，可将R0、S0设计为：

式中：K0是故障检测增益。由于S0输出与R0输出的总和是空间W到U的映射，此总和u0可以表示为：u0=R0（ud）（t）+S0（ya）（t），收到故障信号影响后控制输入ud变为：ud=R-1（e）（t）+uf。式中uf为故障信号引起的控制输入变化量。算子D是ω到ud的映射，故yd等价于受到故障信号后的控制输入[8]。然而直接将u0映射到D是不可行的，因为u0和ω所属于不同的向量空间，故设计单模算子L，使L（S0N+R0D）=I，其中L相当于一个有空间U到W的空间转换算子。则故障检测信号为：abs[R-1（e）（t）-yd]，若没有受到故障信号的影响，则故障信号检测值为0。

图7-2　故障检测算子设计框图