5.3.1　半导体制冷系统模型建立

半导体制冷板各部分具体尺寸如下图5-8所示。根据对象所建立的数学模型为运用物理学定理建立的铝板热过程模型，遵循了能量守恒定律。所用到的物理定理如：傅里叶定律、牛顿冷却定理等[39，40]。

图5-8　铝板尺寸图

（1）傅里叶定律：在热量传导的阶段中，每秒经过预先选取的截面积的热量与该截面法向方向上温度变化率及给定的截面面积成正比，且热量从高温处传向低温处。数学表现形式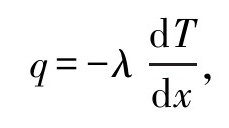：式中q是热流密度（W/m2），λ是导热系数（W/mK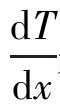），是温度梯度（K/m）。

（2）牛顿冷却定律：该定律用于描述高于环境温度的物体向环境传热并逐步冷却时所满足的规律。当所研究物体与环境具有温差时，在单位时间和面积上热量从高温物体向环境散发的热量与温差值成正比，比例系数叫作热传递系数。该定律主要是牛顿通过实验建立的，实验时在温差不大且强制对流的情况下能够比较好地符合。作为传热学的一个基本定律，它主要的功能是计算对流热量的值。公式为q=αΔT，α是空气的传热系数（W/m2K），ΔT是初始温度与期望温度之间的温差。

（3）比热容定律：单位质量的某种物质，在温度上升1摄氏度的时候所汲取的热量就被叫作是它的比热容，通常用符号c表示。在国际单位制里面，比热的单位为[J/（kg·K）]，也可以是[J/（kg·℃）]。它的数学表达式：Q=cmΔT,Q指的是热量；m为所研究物体的质量，ΔT为物体在经过热量变化后温度的改变量。

（4）热传导定律：在温度非均匀分布的物体中，因温度的差别会形成热传导。物体中耗散的能量满足数学关系：Q=KΔT。在珀尔贴热量耗散的传热过程的研究中，K是热导率（W/K），ΔT是各部位的温度差（K）。

（5）焦耳定律：该定律对传导电流发热情况做了定量的说明。它所涵盖的内容为：传导电流经过导体时所生成的热量与电流大小的平方、通电时间都成正比，与导体的电阻成反比。其数学表现形式是：Q=i2R。针对珀尔贴元件而言，里面的Rp表示的是它的电阻（Ω）。

铝板中心位置向其两侧传递的热量为：

从傅里叶定律可知，铝板和空气之间因为对流而产生的热量为：

根据热传导定律、焦耳定律可知珀尔贴元件总共汲取的热量：

从比热容定律可以明确铝板热量的变化量：

根据热量守恒可知：

则有：

解得本文对象的模型：

式中：s=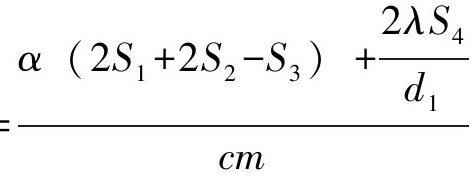；铝板温度的变化量y（t）=T0-Tx；控制输入ud=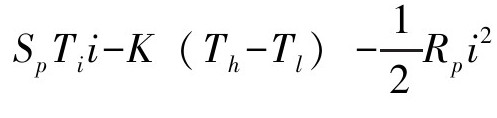，也就是前文中所提到的Q3部分，其中，SpT1i是珀尔贴效应所产生的从吸热面到放热面热量的总体变化量，K（Th-Tl）是不同面温差的热传导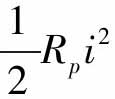，为输入电流对珀尔贴产生的焦耳热。模型中，电流为输入，温度差为输出。

5.3.2　鲁棒精确跟踪控制系统设计

根据需求，本节首先研究了如何利用标称系统与真实系统对观测器进行设计，设计了两个稳定算子控制器：状态观测器S和扰动观测器R，以消除不确定部分对系统造成的影响，使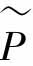等效成标称系统；其次，设计两个满足Bezout等式的稳定的算子控制器A、B，保证系统的鲁棒稳定性；最后，设计精确跟踪控制器C，令系统的输出精确跟踪上其参考输入。

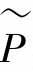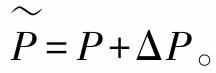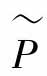图5-9是本节提出的反馈控制系统结构的框架。其中，真实系统为，它包含了两个部分：标称系统P及不确定部分ΔP。即P和分别有右分解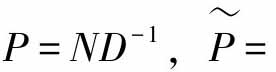：（N+ΔN）D-1。其中，N，ΔN,D都是稳定算子，D可逆，ΔN不明确，但是它的上下界是给出了的。r是系统的参考输入，y称为系统的实际输出。S和R分别为基于算子理论的状态观测器及基于算子理论的扰动观测器，它们的设计是为了消除系统不确定性对实现精确跟踪控制造成的影响，u∗是等效部分P∗的输入。A、B为算子控制器，B是稳定线性控制算子且B可逆。

图5-9　鲁棒稳定精确跟踪控制系统

（1）算子观测器的设计。不确定部分的未知性使得系统难以设计控制器，无法使系统拥有比较理想的性能。因此，本节设计了图5-9中P∗所示的这一块，也就是精确跟踪控制系统的一部分，如图5-10所示。

当基于算子理论的状态观测器S及基于算子理论的扰动观测器R满足条件：

时，P∗等效成标称系统P，系统里面的不确定部分得以消除。其中，I为单模算子。

图5-10　基于算子理论的非线性反馈控制结构

证明：

如图5-10所示，为P∗部分。对图5-10中涉及的带有不确定部分的非线性控制结构，有：

则：

那么，图5-10可以等效为图5-11。

图5-11　图5-10的等效图

对图5-11中的非线性反馈结构，若可以符合式（5-26）中的条件，有：

即：

则，y（t）=P（u∗）（t），且有新的等效P∗=P=ND-1，那么，不确定性产生的副作用得以消除，证明完毕。

（2）精确跟踪控制器的设计。对于图5-9所示带有不确定部分的非线性控制系统来说，若：

AN+BD=M∈u（W,U）

（5-30）

则系统鲁棒稳定。在此基础上，若：

NM-1C=I

（5-31）(www.daowen.com)

那么，可以获得系统的精确跟踪性能。

图5-12　图5-9的等效图

证明：

依据条件式（5-26），图5-10等效为图5-12。根据文献[1]中的鲁棒稳定条件，AN+BD=M∈u（W,U）是单模算子时，则该系统鲁棒稳定。

更进一步地，若AN+BD=M∈u（W,U）为单模算子，则图5-12可等效为图5-13形式。

图5-13　图5-12的等效图

若要使输出跟踪上参考输入，则需：

y（t）=I（r）（t）

（5-32）

对图5-13系统，显然有：

y（t）=NM-1C（r）（t）

（5-33）

根据式（5-33），则需：

NM-1C=I

（5-34）

论证完毕。

至此，精确跟踪控制器的设计得以实现。

根据式（5-26）、（5-30）及AN+BD=I，得观测器：

根据鲁棒稳定条件，得稳定算子控制器：

式中：β为设计的可调的参数。

根据右分解算子N（ω）（t）、D（ω）（t），算子控制器A（y）（t）、B（ud）（t），可以得到：

M=AN+BD=ω

（5-39）

若要满足精确跟踪性能，由式（5-39）可知，只要满足条件CN=I即可。根据式（5-30）、（5-31），得精确跟踪控制器：

从以上两个定理中我们可以看到，半导体制冷系统的不确定部分通过基于算子理论的观测器S、R得以消除。稳定的算子观测器A、B保证了这个单输入单输出（SISO）系统的鲁棒稳定性，精确跟踪控制器C使得系统输出跟踪上了参考输入。

5.3.3　仿真与结果分析

为了说明该方法的有效性，对铝板与珀尔贴组成的半导体制冷装置利用Matlab软件进行了仿真。模型所用的参数列于表5-1。

表5-1　模型参数

表5-2及表5-3给出了本文使用的仿真参数。铝板的初始温度和期望温度分别为21.3℃和18.3℃。模拟时，电流限制输入在0～2.2A之间。在模拟过程中，我们设置的参考输入r=3，此为期望铝板利用珀尔贴元件下降的温度值，这意味着铝板最终需要比初始温度下降3℃。制冷装置的模型不确定性及外部扰动均认为在ΔN中，且ΔN=0.5+0.5×sin（100πt）。

表5-2　仿真参数

表5-3　仿真参数

文献[40]运用了近似跟踪控制的方法。图5-14展示出了该方法的输入过程的仿真结果，图5-15展示出了其温度输出过程的仿真结果。运用本文提出的精确跟踪控制方法，图5-16展示出了控制输入下的仿真结果，图5-17展示出了输出的温度变化过程的仿真结果。通过对比，我们可以发现，两种方法均可使系统的鲁棒稳定性得以保证，跟踪性能也得以实现。但是，本节提出方法的仿真轨迹要比根据在文献[40]中提出的方法的仿真轨迹更平滑，超调时间更短。因此，通过仿真结果可以证明，通过基于算子理论观测器的设计、精确跟踪控制器的设计，在非线性系统存在不确定部分的前提下，仍旧可以保证鲁棒稳定，并且实现跟踪性能，使半导体制冷装置快速、精准、稳定地下降到预期温度。

图5-14　文献[40]输入过程

图5-15　文献[40]温度输出

图5-16　本文提出方案的输入过程

图5-17　本文提出方案的温度输出