机器人手臂作为典型的非线性系统,不仅具有多个输入多个输出,而且在其输入输出之间具有耦合现象[4~30]。为了应用基于演算子的鲁棒右互质分解技术,应用压缩原理将耦合影响等效成为不确定性的因素,得到具有不确定性的多输入多输出的非线性动力学模型。首先研究了如何通过标称模型与真实模型设计观测器来抑制不确定性的影响。设计基于标称模型的稳定控制器,来抑制不确定性的影响,使其等效的模型P∗=P,在这里控制器S和R的可行性将为论证。其次,设计控制器A和B,并且根据基于鲁棒右互质分解的鲁棒稳定条件(AN+BD=I)进行鲁棒稳定性分析。
对于含有不确定性的机器人手臂,通过使用鲁棒右互质分解和前置算子方法,提出基于演算子理论的鲁棒跟踪控制框图。图5-1中的鲁棒非线性跟踪控制结构框图,整体模型是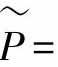
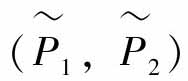 ,其中包括两个部分,标称模型P1=(P1,P2)以及不确定模型ΔP1=(ΔP1,ΔP2),也就是说
,其中包括两个部分,标称模型P1=(P1,P2)以及不确定模型ΔP1=(ΔP1,ΔP2),也就是说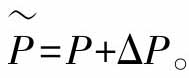 假设标称模型P和整体模型
假设标称模型P和整体模型 都有右分解,即
都有右分解,即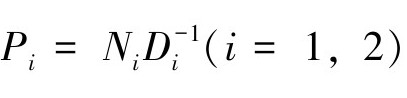 和
和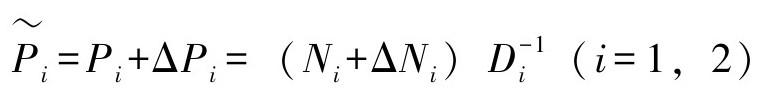 ,相应地,
,相应地,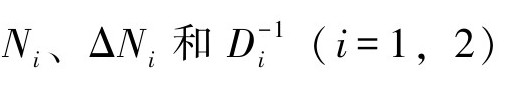 是稳定的算子。Di是可逆的,ΔNi是未知的,但是其上下界是已知的[31~38]。r=(θ1d,θ2d)和y=(θ1,θ2)分别是参考输入和模型输出,对应u=(u1,u2)是关节力矩的控制输入。算子控制器S和R被设计用来抑制模型的不确定性的影响。u∗=(u1∗,u2∗)是等价模型P∗的输入。A和B分别是算子控制器,且B是稳定且可逆的线性算子控制器。下面将解释如何设计算子控制器S和R来抑制不确定性的影响,并且如何设计算子控制器A和B来保证鲁棒稳定跟踪。
是稳定的算子。Di是可逆的,ΔNi是未知的,但是其上下界是已知的[31~38]。r=(θ1d,θ2d)和y=(θ1,θ2)分别是参考输入和模型输出,对应u=(u1,u2)是关节力矩的控制输入。算子控制器S和R被设计用来抑制模型的不确定性的影响。u∗=(u1∗,u2∗)是等价模型P∗的输入。A和B分别是算子控制器,且B是稳定且可逆的线性算子控制器。下面将解释如何设计算子控制器S和R来抑制不确定性的影响,并且如何设计算子控制器A和B来保证鲁棒稳定跟踪。
图5-1 机器人手臂系统的跟踪控制图
5.2.1 算子观测器
由于不确定模型ΔP的未知导致很难设计算子控制器来获得理想性能。为了解决这一问题,基于演算子的理论,算子观测器作为鲁棒非线性控制系统的一部分被设计出来,并且显示如图5-2所示,且满足:
也就是说,
因此,图5-2中的方框图等效于图5-3。
图5-2 基于算子理论的非线性反馈控制框图
图5-3 图5-2等效框图
基于Lipschitz算子的概念和压缩映射定理,根据下面的条件设计算子控制器S和R,可以抑制不确定性的影响。
提出的含有不确定性的非线性控制系统如图5-2所示,如果:
这个新的等价模型P∗=P,不确定性的影响被抑制,这里的I是单模算子。
证明:对于如图5-3所示的非线性反馈系统,如果可以满足式(5-3)中的条件,可以推出:
即:
式中:y(t)=P(u∗)(t);并且新的等价模型P∗=P,不确定性的影响被抑制,证明完毕。
5.2.2 跟踪控制设计
提出的含有不确定性的鲁棒非线性精确跟踪控制框图,如图5-4所示,如果:
那么既可以保证系统的鲁棒稳定,而且可以保证跟踪性能。
证明:根据条件(5-5),图5-1可以等效成图5-4。根据文献[5]给出的鲁棒稳定条件,我们可以发现,如果AN+BD=M∈u(W,U)是单模算子,鲁棒稳定条件可以得到满足。
此外,如果AN+BD=M∈u(W,U)是单模算子,那么图5-4可以等效成为图5-5。对于图5-3显示的鲁棒非线性精确跟踪控制系统,如果满足条件(5-5),则:
这样,模型的输出y可以跟踪参考输入r,证明完毕。
图5-4 图5-1的等效框图(https://www.daowen.com)
图5-5 图5-4的等效框图
根据定理1和定理2,我们可以发现,不确定因素的影响可以通过本章提出的算子观测器来抑制。鲁棒稳定可以通过设计基于算子的稳定控制器A和B来保证,跟踪性能可以通过设计PI系统得以保证。
5.2.3 算子控制器设计
图5-1的框图可以等效为图5-4。根据Bezout恒等式AiNi+BiDi=Ii,(i=1,2),稳定的算子控制器可以得到如下:
式中:βi是设计的参数。
根据设计出的右分解算子Ni(ωi)(t),Di(ωi)(t)和B-1(e)(t),下面的等式成立:
式中:Mi是单模算子,因此,在NM-1C=I条件满足情况下,输出y=(y1,y2)可以跟踪参考输入r=(θ1d,θ2d)。下面设计跟踪控制器C,即PI跟踪控制器,即比例积分控制器,形式如下:
式中:Kαi,Kβi,i=1,2是设计的参数;Kβi是积分系数;Kαi是比例系数。
本方法的主要亮点:首先,扩展了文献[5]的实现方式,即得到精确跟踪。第二,考虑到不确定模型ΔP是未知的情况下,推导出来有限制的所谓的通用条件,即在满足NM-1C=I的条件下,输出y=(y1,y2)可以跟踪参考输入r=(θ1,θ2)。在本章中,通过设计算子观测器和满足给定条件(5-5),不确定性影响被抑制。精确跟踪可以由公式(5-7)来到保证。
5.2.4 仿真与结果分析
为了验证上述方法可以有效地抑制了非线性系统中存在的不确定模型的影响,并且实现精确跟踪的控制效果,本章的仿真对象仍然以两连杆的机器人手臂为模型[31]。其物理和结构参数分别为:
机器人手臂的标称模型已经给出。然而在实际控制中,无法获得li、lgi和mi的真实值,即结构参数Zi是未知的。因此,在仿真中,机器人手臂的不确定参数当作:
式中:Z∗i被假设成真实值。此外,扰动为:
扰动和不确定的结构参数被归纳成ΔN。仿真中,角速度的初始条件是:
角加速度的初始条件是:
在仿真中,设计的参考轨迹是半圆形的轨迹:
从起始位置(xd,yd)=(0.6,0)(m)运动到终点位置(xd,yd)=(-0.6,0)(m),这里笛卡尔变量(x,y)和关节角度(θ1,θ2)的关系在文献[28]中有所描述。图5-6(a)中显示的是通过使用上一章提出的控制理论方法仿真得到的端点位置的跟踪结果,端点轨迹的误差跟踪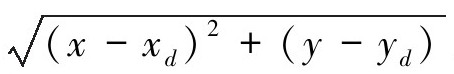 显示在图5-6(b)中。图5-7(a)中显示的是使用本章提出的控制方法的仿真方法得到的端点位置跟踪结果,端点轨迹的误差跟踪显示在图5-7(b)中。
显示在图5-6(b)中。图5-7(a)中显示的是使用本章提出的控制方法的仿真方法得到的端点位置跟踪结果,端点轨迹的误差跟踪显示在图5-7(b)中。
图5-6 使用第四章方法得到的仿真结果
通过分析图5-6和图5-7,我们可以发现基于建议方法的仿真轨迹比使用上章节提出的方法的仿真轨迹更为平滑,机器人手臂的末端轨迹的误差减小了75%,实现了精确跟踪控制。
图5-7 使用本文提出的方法得到的仿真结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





