滑模控制最基本原理是根据系统运行的动态要求来设计合适的滑模面，通过滑动模态控制器使系统状态从滑外的任意一点趋近于滑模面，在控制律的控制下，使得系统沿着滑模面运行，并且保证系统可以在平衡点处稳定，这一过程称为滑模控制，也常常称为滑模变结构运动。通过系统所需要达到控制参数或者理想的动态特性来设计滑模控制系统中的滑模面，在有限时间内迫使系统进入并且维持在设计好的滑模面上进行运动。此外，滑模控制的优点还有响应速度快、控制结构简单、良好的鲁棒性能等。

滑模控制的缺点是当系统维持在滑模面两侧运动时，其高频开关反馈控制导致了抖振的产生。由于滑模变控制使系统不断地穿越滑膜面运行，所以在本质上它是一类无法进行连续控制的非线性控制方法。抖振现象限制了滑模控制的实际应用的范围，这是因为它容易导致系统未建模的动态特性，严重地影响了控制性能[4，5]。

由于滑模控制系统所具有的上述优点，所以在机器人手臂的跟踪控制系统的设计中广为应用。一方面，滑模面设计的不断优化和创新，使得机器人手臂的控制进一步取得了良好的性能；另一方面，滑模控制结合不同算法例如模糊控制、神经网络控制等方法来抑制或者减小抖振现象。在研究中，将滑模控制和鲁棒右互质分解方法相结合，首先用右互质分解对两连杆的机器人手臂进行模型分解，然后设计稳定算子控制器，以保证系统的鲁棒稳定，再设计基于滑模控制的跟踪控制器，改善系统的跟踪性能，加速跟踪速度。

本研究中，对传统的指数趋近律进行改进，使系统得到更好的跟踪性能，不仅缩短运动点到达滑模面的趋近时间，而且抑制系统抖振现象。图4-1是非线性系统反馈跟踪控制的框图。

在本研究中，以含有不确定性的两输入两输出的刚性机器人手臂为具体的研究对象[6～24]，实际模型是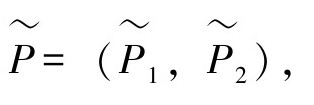它其中包括两个部分，标称模型P1=（P1，P2）以及不确定模型ΔP1=（ΔP1，ΔP2），也就是说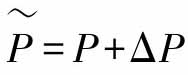。名义模型P和整体模型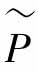假设都有右分解，满足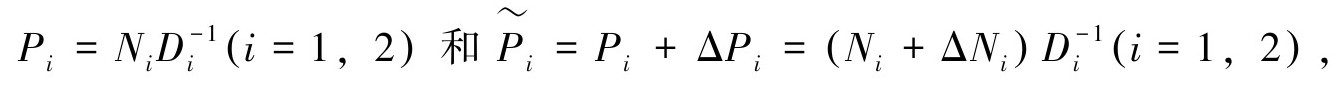其中，Ni和Di（i=1，2）都是稳定的算子，Di是可逆的，ΔNi是未知的，但是其上下界是已知的。

图4-2　非线性系统反馈跟踪控制

对于式（3-1）表示的两连杆机器人手臂的动力学模型，该非线性系统可以右互质分解，分解出来的算子分别为Ni和Di，Ni（ωi）（t）=ωi（t），i=1，2，Di的形式如下：

由于此处研究的是含有扰动和模型不确定性的非线性系统的鲁棒控制问题，因此给定一个对N的扰动信号，即ΔN。这里的算子Ni和Di是稳定的，且Di是可逆的。

右分解中的Ni和Di的设计都是基于名义模型。然而，在实际情况下，除了结构参数Zi，Z2和Z3引起的模型误差，外部扰动也是不可避免的。本文的控制系统设计，模型误差和扰动对于系统性能的影响被认为是机器人的动态不确定性。针对机器人的不确定性，这里研究如何基于演算子理论的鲁棒右互质分解方法设计机器人手臂的鲁棒非线性控制器，如何实现良好的跟踪性能。

根据右互质分解条件和鲁棒稳定条件，稳定的算子控制器可以得到：

式中：βi是设计的参数。(www.daowen.com)

下面通过滑模控制讨论在鲁棒稳定下如何实现精确跟踪。在滑模控制下，系统的轨迹运动过程通常分成两个部分：趋近过程和滑模过程。该系统从滑模面外的任一初始位置，最后到达滑模面的运动过程被称为趋近运动。而滑模运动是指系统在滑模面上保持滑行的过程，在滑模运动的阶段，系统误差可以逐渐收敛为零，误差收敛的速度可以通过改变滑模面中的常数矩阵C来进行优化。

在滑膜控制中，滑模到达条件仅仅可以保证平面上的任意点可以在有限的时间内达到滑模面控制的要求，但对于在这一过程中，运动轨迹的具体形式没有任何限制。关于系统怎样达到滑模面的轨迹跟踪问题，高为炳院士提出趋近律这一概念，通过选择合适的趋近律，就可以把求解不等式的问题转变成为求解代数方程的问题，从而达到了期望的动态品质，这一概念的提出可以大大地缩短趋近时间并且抑制抖振现象的发生。

在滑模控制理论中，稳定的系统将保持在滑模面上运行。基于滑模趋近律控制系统的设计步骤如下：首先选择一个滑模面s；然后设计控制率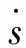使得状态变量在滑模面上运行并且保持持续的运动；最后联立方程求解出来控制律。

θi为参考输入信号，输出跟踪误差e为：

e（t）=θd-θi　i=1，2

（4-6）

误差e的微分形式如下：

该系统的轨迹被限制在滑模面时，可以保证期望的跟踪效果。在本研究中，滑模面被定义为：

式中：c1＞0和c2＞0，并且c1和c2满足赫维茨稳定性条件。

应该注意的是，滑模面函数的阶数小于系统原来的阶数。滑模控制并不决定于模型自身的动态方程，而是由滑模面中的参数C决定的。因此，s的微分形式为：