3.2.1　机器人手臂系统

机器人手臂的控制系统是控制机器人性能的核心部分，其控制技术制约着机器人技术的发展。随着科技的发展，更多工作需要高精度、响应速度快的机器人完成，这也使机器人向快速响应、高精度方向发展，因此机器人手臂的控制是一个非常具有挑战性的问题[4，5]。

对于机器人手臂的控制，很多控制方法被相继提出。PID控制是一种应用最为广泛的控制方法，但是由于被控系统经常存在不确定性或者无法得到精确的模型，因此无法得到理想的控制性能。为了改进性能并设计鲁棒跟踪控制系统，很多控制方法被相继提出，如最优控制、学习控制、自适控制、滑模控制等[6～24]。然而，最优控制理论需要一个精确的模型，但是对于含有非线性动态的“复杂”机器人系统很难对其进行系统辨识，而且高维状态空间很难求解。对于学习控制方法，由于状态和控制动作空间的组合爆炸，很难实现基于强化学习算法的学习控制理论。自适应控制的缺点是当存在不确定性的条件下，无法保证系统的稳定性。这是因为该算法需要不断检测系统的各项参数，然后自发地调节控制器的参数，这也就意味着此方法需要满足实时控制的要求。滑模控制也经常被称作滑模变结构控制，由于系统本身的不连续控制导致的控制器频繁切换，很容易引起抖振现象，进而造成机械磨损，影响使用寿命，其优点是对于不确定系统有非常好的鲁棒性。神经网络控制算法不仅有很强的容错性能，而且有良好的自适应学习的能力，因此有很快的运算能力，可以很好地处理非线性系统中存在的不确定性的问题；但是也正是由于其自学习能力强，使得当环境发生改变的时候，就需要重新学习。因此，不断研究并改进控制系统的性能，是一个重要的研究方向。因而，探索好的方法不断提高控制系统的性能仍是当前一个重要的研究方向。基于演算子理论的鲁棒右互质分解方法是一种新型的控制方法，可以很好地处理非线性系统的鲁棒控制这一问题。特别是对于含有模型不确定性或者容易受到外界扰动影响的非线性系统的控制系统分析和设计是一种很有前途的方法。

机器人手臂是可以模拟人臂运动功能的机械机构，通常由多个关节组成，一般采用电机驱动各关节。通常情况下，可以将机器人手臂看成由开链式的刚性多连杆机构构成的系统，各个关节也看作是理想的几何约束关节[25，26]。连杆运动是通过各个关节间的运动进行带动的，使得机器人手臂的末端快速精确地运动到指定的位置。机器人手臂的始端关节通常固定在基座上，末端通常为执行器，根据控制的需要安装各种执行器用来实现各种操作功能。对于机器人手臂系统自身而言，其模型描述包括动力学模型和运动学模型。运动学研究机器人手臂相关的运动性能，主要研究的内容是个刚性连杆位置坐标、姿态坐标系的建立和不同坐标间的变换关系。而动力学则研究机器人手臂的角度、角速度、角加速度等运动变量与力、力矩的关系。机器人手臂的动态性能不仅与运动学因素有关，还和机器人手臂的分布质量、形式结构、执行机构的位置等因素有关。

目前，对于机器人手臂动力学建模，提出了很多的方法[26]。其中建立动力学模型的最根本目标是：有效消除各个关节之间的耦合作用、建立系统运动参数和关节驱动力之间的简洁明了的函数关系式。具体的控制算法包括高斯原理法、牛顿欧拉方程法以及凯恩斯方程法。高斯原理法运用最小约束原理，用求极值的优化算法求解机器人手臂的运动参数。牛顿欧拉法是建立在牛顿第二定律的基础上，对于机器人手臂的平动和转动可以分别用牛顿方程和欧拉方程来建立。凯恩方程法无需求解繁琐的关节的约束力，就可以有效地求解出来连杆的速度、加速度及关节驱动力，求出关节驱动力仅仅需要进行一次性的推导，因此提高了计算的速度，其完整的结构很适用于对闭链机器人的进行动力学的建模。本文所采用拉格朗日方程的方法，以整体的机械系统作为控制对象，着眼于对整个系统的能量概念，利用动、势能变化关系来建立动力学模型，无需去求解运动学中的物理量，因此更适合比较复杂的机器人系统的模型建立。

动力学的研究通常涉及两个最基本却截然相反的问题，一个问题是已知机器人手臂的运动轨迹，求各关节的驱动力矩，即动力学逆问题；另一个问题是已知机器人手臂各关节的驱动力矩或者驱动力，求机器人手臂运动参数和轨迹，称之为动力学正问题。

两连杆刚性机器人手臂的结构如图3-3所示，动力学模型通常是用非线性二阶微分方程来表示[26～30]：

这里的I和H分别表示惯性转矩2×2（）以及科里奥利离心力矢量，且：

式中：

图3-3　两连杆机器人手臂的结构图

式中：mi表示杠杆i的质量；lgi表示关节i和连杆i的质点之间的距离；Ii代表连杆i的转动惯量；li表示连杆i的长度；Z1、Z2和Z3分别表示机器人手臂的物理特征结构参数。

由上可知，方程式（3-1）是复杂且时变的非线性系统，这里角位置、角速度、角加速度分别用表示，是个连杆i的连接角，。是连杆i的控制转矩输入，对于本节运用的模型，一共有两个驱动力矩τ1和τ2，第一关节驱动力矩τ1作用在底座和连杆1之间，第二关节驱动力矩τ2作用在底座和连杆2之间，τ=（τ1，τ2）。

3.2.2　基于右互质分解的机器人手臂的鲁棒控制

在本节中，以含有不确定性的两输入、两输出的刚性机器人手臂为具体的研究对象，基于右互质分解的机器人手臂反馈控制系统框图如图3-4所示，实际模型是，它包括两个部分，标称模型以及不确定模型也就是说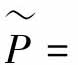P+ΔP。名义模型P和整体模型假设都有右分解，满足和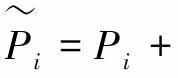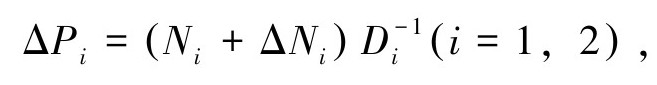式中，Ni和Di（i=1，2）都是稳定的算子，Di是可逆的，ΔNi是未知的，但是其上下界是已知的。

图3-4　基于右互质分解的机器人手臂反馈控制系统

对于式（3-1）表示的两连杆机器人手臂的动力学模型，该非线性系统可以右互质分解，分解出来的算子分别为Ni和Di，Ni（ωi）（t）=ωi（t），i=1，2，Di的形式为

由于本书研究的是含有扰动和模型不确定性的非线性系统的鲁棒控制问题，因此给定一个对N的扰动信号，即ΔN。这里的算子Ni和Di是稳定的，且Di是可逆的。

右分解中的Ni和Di的设计都是基于名义模型。然而，在实际情况下，除了结构参数Zi，Z2和Z3引起的模型误差，外部扰动也是不可避免的。这里的控制系统设计、模型误差和扰动对于系统性能的影响被认为是机器人的动态不确定性。针对机器人的不确定性，这里研究如何基于演算子理论的鲁棒右互质分解方法设计机器人手臂的鲁棒非线性控制器，如何实现良好的跟踪性能。

根据右互质分解条件和鲁棒稳定条件，稳定的算子控制器可以得到：

式中：βi是设计的参数。

3.2.3　基于PI的跟踪控制器设计(www.daowen.com)

为了不断地提高机器人手臂的工作性能，以满足日益高标准的生产和生活的要求，必须不断提高机器人手臂的控制系统性能，其最终目的是使其末端按照参考的轨迹快速精准的运动，这也是机器人手臂控制最为重要的任务。对机器人手臂的轨迹进行跟踪控制是指通过控制算法计算出来需要的各关节驱动力，使得机器人手臂的运动变量按照理想的信号运行。当其期望轨迹是连续变化的曲线时，则称之为轨迹跟踪控制。

根据上面章节可知，首先运用鲁棒右互质分解方法对非线性系统进行分解，然后根据分解结果设计稳定算子，可以保证系统的稳定性。然而跟踪问题也是我们必须考虑的问题，对于已经稳定的非线性系统，为实现跟踪功能，设计非线性反馈跟踪系统的控制框图如图3-5所示，其中虚线内为鲁棒稳定的系统，r=（θid，θ2d）是参考的输入信号，y=（y1，y2）输出信号，是对于已稳定的系统的控制输入，是误差信号。为了使输出y=（y1，y2）

可以跟踪参考输入设计了跟踪控制器C，即PI跟踪控制器，PI是比例积分控制，形式如下：

图3-5　非线性反馈跟踪系统

式中：

Kαi和Kβi中，i={1，2，3，……}是设计的参数；Kβi是积分系数；Kαi是比例系数。

这里的误差信号为，I是单位算子。很明显，和y的空间是一样的，也就是说，指数迭代定律的条件也成立。要保证稳定系统须满足下面的条件：

C是稳定的，并且当T≥t≥t1≥0，r＞0时，

对于任意的x,y∈Vs和t∈（0，T]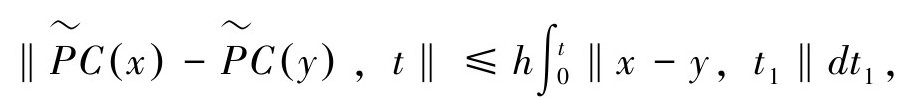，h是PT的增益，可以为任意的常数。

3.2.4　仿真与结果分析

为了验证上述方法的有效性，本章的仿真对象以两连杆的机器人手臂为模型。其物理和结构参数分别为：

即得到机器人手臂的名义模型。然而在实际控制中，很难获得li、lgi和mi真实值，即结构参数Zi是未知的，无法得到完全精确的模型。因此，在仿真中，机器人手臂的不确定参数当作Zi=Z∗i±ΔZ∗i，Δ=0.5，这里的Z∗i被假设成真实值。此外，外部扰动为τd=0.5+0.05×sin（100πt）。扰动和不确定的结构参数被归纳成ΔN。仿真结果如图3-6所示。

仿真中，连杆l1和l2角度的初始条件是：

连杆l1和l2角速度的初始条件是：

模型右分解设计的参数为：

跟踪控制器设计的参数分别为：

参考输入的角位置为：

参考输入的角速度为：

图3-6　仿真结果

图3-6（a）和（b）显示了运用PI控制设计的控制器的仿真结果，连杆l1和l2各自的角度和角速度的输出结果。我们可以发现，系统具有较好的鲁棒稳定性，说明系统的右互质分解是有效的，控制器A和B的设计能达到了要求。此外，我们还可以发现，经过0.8s，角度才可以跟踪上期望信号；对于角速度，响应时间需要1.1秒。由于机器人手臂需要高精度的控制和快速响应的能力，才可以满足不同的任务需求，达到理想的跟踪性能。