对应图2-5基于演算子理论的非线性反馈控制系统可以保证系统的鲁棒稳定，但是不能保证跟踪，另外根据式（2-14）可知，设计精准的跟踪控制器是不可能的。因此，为了能够跟踪给定输入，在系统滑模鲁棒稳定的基础上，设计了外环PI控制器，如图3-1所示，实现精确跟踪控制，并用算子理论证明了该方法的可行性。其中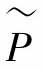代表图2-5鲁棒稳定系统[1～3]。

误差信号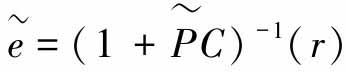，算子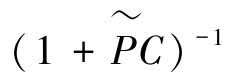是Y到Y的映射。因此，参考信号r和误差信号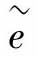的联系是在线性空间。指数迭代理论条件之一得到满足，进而设计控制器，开环控制系统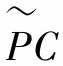等效PT为外加一个积分器，如图3-2所示，并满足以下条件：

图3-1　跟踪控制系统

图3-2　图3-1的等效框图

（1）对所有的t∈[0，T]，C是稳定的，当r＞0，T≥t≥t1≥0，有PT（r）≥K1≥0。

（2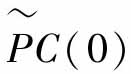）=0。

（3）在所有属于空间Ys的x,y，并且t∈[0，T]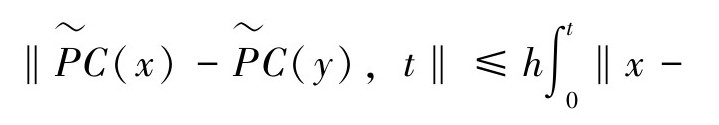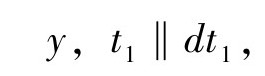，h是任意常数，从输入r到输出y，定义一个算子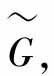反馈方程为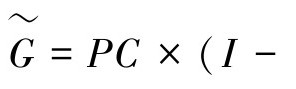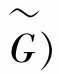。指数迭代理论概括为，如定义1所述：

3.1.1　定义1

在t∈[0，T]，反馈控制方程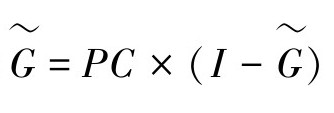）在所有算子都是自身映射的Banach空间中，对于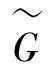拥有唯一的解。条件（2）和（3）满足，模型输出有界。(www.daowen.com)

定义1指出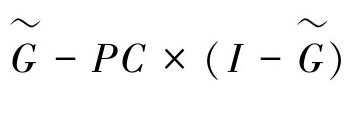）=0，并且有唯一解，那么模型的输出则有界，进而（I+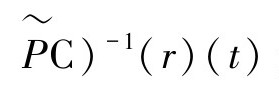是存在的。

3.1.2　定义2

当T≥t足够大时，误差信号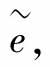即y（t）-r（t）可以任意小。

证明：

因为I为恒等算子，取I（r）=r，有：

当T≥t≥t1≥0，有PT（r）≥K1≥0。得到：

当T≥t，通过取T可以使得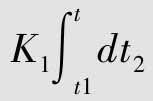任意小。进而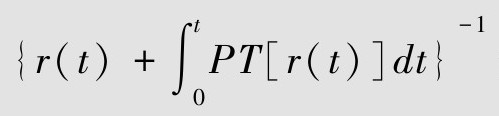，任意小。最终y（t）-r（t）任意小。