针对非线性系统建立的数学模型，是影响控制器设计的主要因素，也是其设计的重要依据。然而，因为非线性系统建模过程中具有参数不确定性（由于参数的变化而引起的模型参数改变）、结构不确定性以及外部扰动等问题，所以会令得到的系统数学模型与真实系统之间有所不同。控制系统内、外部的各种不确定性，令非线性系统鲁棒性能方面的探究变得非常关键。系统的鲁棒特性，表示的是系统能够抵制不确定性的水平。通俗地说，鲁棒性能的研究主要就是为了应对系统不确定性的问题。其中不确定性是对于系统局部的不完全认识，未必就是绝对的无认知或者是完全没有规则的变化。拥有较好的鲁棒性能，则可确保控制系统尽可能小地受到不确定性对系统稳定的影响。也就是说，系统的鲁棒控制，就是在具有不确定性的前提下，系统的稳定性仍然可以得以保障。鲁棒控制的实质性目的，是在模型并不够精准且有来自外界干扰的前提条件下，如何找出一个合适可用的方法，使得系统能够稳定并达到对控制性能的需求。

右互质分解技术目前在线性系统方面的发展已经较为成熟。其理论研究已比较深入，应用方面也得到了极大的推广，因此，该方法在线性系统中得到了广泛认可。但是，对于非线性系统而言，由于系统本身中一些无法避免问题的存在，例如时滞、不确定性、多变量、多约束条件等许多问题，因此，这种方法在非线性控制系统中的运用遭受了层层阻碍。然而，世界各国的专家学者克服种种困难，使得该方法在非线性系统理论中得以推广，并应用在实际系统中，取得了一定的成果。在具有未知不确定性的情况下，若是这个不确定性有界，文献[45]给出了右互质分解技术保证非线性控制系统鲁棒稳定性的条件；为了抑制系统不确定部分对控制系统造成的影响，文献[46]针对带有未知不确定部分的非线性控制系统，运用鲁棒右互质分解技术，给出了一个基于空集概念的充分条件，不过因为不确定部分的未知性，使得该条件的实现极具难度。针对这个问题，文献[45]给出了Lipschize不等式，令鲁棒稳定的条件变得简单。以下部分为鲁棒右互质分解的相关介绍及定义。

图2-7中虚线部分P代表真实系统，ΔP为真实系统中的不确定部分，令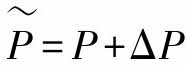。若含有未知不确定部分的真实系统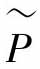具有右互质分解：

则称标称系统P具有鲁棒右互质分解特性。

式中：ΔN=ΔP·D。在研究非线性系统的鲁棒性时，我们可以默认为系统的不确定部分均归为算子N内，即N→N+ΔN。

图2-7　基于演算子理论的鲁棒右互质分解控制系统（单输入单输出）

基于Lipschitz算子的概念，在文献[20]中提出了含有不确定性的非线性反馈控制系统，其控制框图如图2-4所示，U和Y表示给定模型算子P的输入输出空间，例如，P：U→Y,r和y分别是系统的参考输入和系统输出。标称模型和不确定模型分别是P和ΔP，真实模型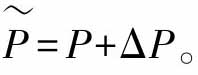标称模型P和真实模型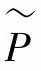的右分解分别为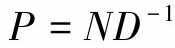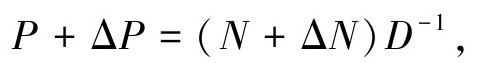，这里的N、ΔN和D都是稳定的算子，且D是可逆的，ΔN是未知的，但是上下界是已知的。此外，这个分解是互质的，或者说P具有右互质分解，如果存在两个稳定的算子A：Y→U和B：U→U满足Bezout恒等式：

AN+BD=M

（2-17）

假设非线性稳定算子P存在右互质分解P=ND-1，N：W→Y,D：W→U，其所受的未知扰动为ΔP：U→Y。在N上的扰动为ΔN=ΔP·D。若有：ΔP·D是稳定的映射，则算子P在未知扰动ΔP下是鲁棒稳定的，或称算子P在ΔP下具有鲁棒稳定性[9～16]。即P+ΔP=（N+ΔN）D-1。

通常，并不硬性要求算子P是稳定的。则有以下定理：

假设算子P：U→Y存在右互质分解P=ND-1，且其所遭受的未知扰动为ΔP：U→Y，在N上的ΔN=ΔP·D。若未知扰动ΔP为是稳定的，那么在ΔP的影响下，依旧能够鲁棒右互质分解[17～21]。

假设算子P：U→Y存在右互质分解P=ND-1，且其所遭受到的未知扰动为ΔP：U→Y，在N上的ΔN=ΔP·D。ΔP=ΔN·D-1是右互质分解也就表示P+ΔP=（N+ΔN）D-1具有同样的效果。

基于Lipschitz算子的定义，文献[45]给出了带有不确定部分的非线性反馈控制系统，即图2-7所示系统。U和Y分别代表非线性算子P的输入、输出空间，P：U→Y。r为系统的参考输入，y为系统的输出。系统建立的数学模型P称为标称系统，P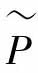为真实系统，由标称系统P和系统不确定部分ΔP构成。标称系统的右分解为P=ND-1，真实系统的右分解为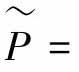P+ΔP=（N+ΔN）D-1。N、ΔN和D全部为稳定的算子，D可逆。ΔN不明确，但是它的上下界是给出了的。若有稳定的算子A和B，使得A、N、B、D满足Bezout等式：(www.daowen.com)

AN+BD=M

（2-18）

则算子P具有右互质分解。其中，B可逆，M∈（W,U）为单模算子。

在式（2-15）的基础上，若有：

那么，这个系统就是单输入单输出（SISO）稳定的。即该非线性系统是鲁棒稳定的[141]。

其中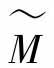，为单模算子。

当满足式（2-18）时，在式中的A（N+ΔN）+BD=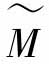∈u（W,U）隐含了图2-7系统的一个条件：

从式（2-19）中可以发现，如果有（N+ΔN）M-1=I，则系统输出跟踪上了参考输入。但是在真实环境中，ΔN一般都是未知的。所以，想要符合（N+ΔN）M-1=I这个条件难度非常大。因此，在后续的章节中会针对这个问题进行研究，也就是在考虑保证非线性系统鲁棒稳定的前提条件下，如何设计精确跟踪控制器。

类似地，基于演算子理论的鲁棒右互质分解理论，考虑到不确定性的影响下，提出了多输入多输出的非线性系统的鲁棒控制反馈系统[22，23]。假设标称模型P和真实模型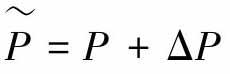有右分解，即P=ND-1和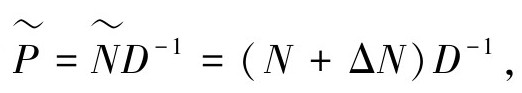也就是：

式中：Ni、ΔNi和Di是稳定算子；Di-1是可逆的；ΔNi虽然未知，但已知其上下界。因此，对于含有不确定性和耦合效应的多输入多输出的非线性系统，标称模型和真实模型分别满足Bezout恒等式：

这样鲁棒BIBO稳定性可以保证，通过满足：

需要注意最初状态应被考虑，即AN（w0，t0）+BD（w0，t0）=M（w0，t0）应该被满足。在本节中，选取t0=0和w0=0。

图2-8　含有不确定性的多输入多输出非线性反馈控制系统