基于算子理论的右互质分解技术不被输入信号的形式所牵制，现已成为解决非线性控制系统的分析和应用等问题的有效方法。以下将给出该方法的相关定义。

2.2.1　定义8：反馈控制系统的适定

对于一个反馈控制系统，如果组成系统的每个环节都是因果的，而且对给定的输入，系统内部的每个信号都是唯一被确定的，那么就称这个系统是适定的。

2.2.2　定义9：算子的右分解

如图2-3所示，如果具有因果稳定的算子N：W→Y,D：W→U,D在U上可逆，且满足等式[7～10]：

图2-3　算子P的右分解

则认为算子P存在右分解。如果N与D均为稳定的算子，则P被认为存在稳定的右分解。

算子D：W→U可逆是算子P具有右分解的充分必要条件，并且D（Ws）⊂D0（P）。

证明：必要性：设P有右分解P=ND-1。∀u∈D（Ws）⊂Us，∃w∈Ws，使得u=D（w），从而P（u）=PD（w）=N（w）∈Ys。所以u∈Us∩G-1（Ys）=D0（P），从而有D（Ws）⊂D0（P）。

充分性：若存在D：W→U可逆，且D（Ws）⊂D0（P）。则：

（1）D（Ws）⊂Us，D稳定；

（2）作N=PD：W→Y。∀w∈Ws，D（w）∈D（Ws）⊂D0（P）⊂P-1（Ys），所以N（w）=PD（w）∈Ys。N稳定。

所以P=ND-1，N、D稳定。论证完毕。

基于算子理论的非线性右互质分解技术，有两种理论方法：一种是关于输入—输出理论，另一种是基于Bezout等式的理论。

例如，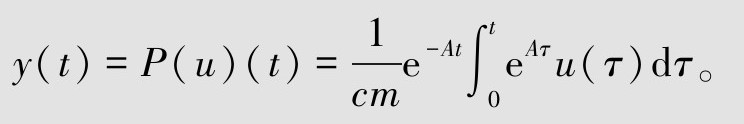

取算子D：W→U：u=D（w）=cmw，是线性放大器，故算子D是稳定的且在U上可逆，其逆算子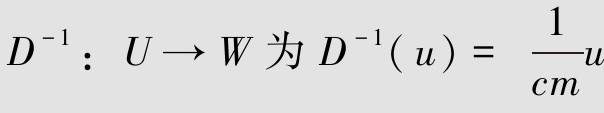。取算子N：W→Y为：y=N（w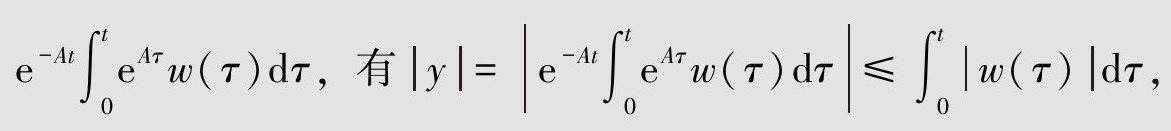）=可见算子N：W→Y是稳定的。不难验证，对任一输入信号函数u∈U有：

即P=ND-1。

2.2.3　定义10：算子的右互质分解

如果P存在右分解P=ND-1，且N和D在W上没有伪状态，则称P存在右互质分解。(www.daowen.com)

所谓W上的伪状态w，是指w∈W-Ws，使得N（w）∈Ys，且D（w）∈Us，如图2-4所示[5]。

图2-4　算子分解的伪状态

另外，设N和D是P的f.g.稳定的右分解。如果D（Ws）=D0（P），且存在α＞0，使得：

则称这个f.g.稳定的右分解是互质的。

此处在对系统进行右互质分解时，用到的是基于Bezout的方法，有关Bezout方法下非线性算子的右互质分解，是基于图2-4所示的非线性反馈控制系统，设算子P有右分解P=ND-1，若能找到两个稳定的算子A：Y→U,B：U→U，满足Bezout等式：

AN+BD=M

（2-12）

式中：B可逆；M∈μ（W,U）为单模算子，则称P存在右互质分解，也可以称分解是互质的[7，9，10]。

一般地，P并不稳定，算子A、N、B、D均为被设计的对象。另外，值得我们留心的一个地方是，应当注意到系统的初始状态，要求符合条件式（2-13）：

图2-5　基于演算子理论的非线性反馈控制系统

Bezout方法的实质为：利用右互质分解技术将一个非线性算子以两个非线性稳定算子“比”的形式表示出来，再相应地找出两个稳定算子，与上述提及的算子一起满足Bezout恒等式。Bezout方法能够对系统鲁棒稳定、跟踪控制等方面的一些难题有比较优良的解决办法，并且Bezout等式里面的相关参数能够被用作构建控制器。但是，该方法的缺点是对于Bezout等式的求解过程较为困难繁杂。

2.2.4　定义11：幺模（阵）算子

设图2-5中的控制系统是适定的，如果系统有右分解P=ND-1，那么系统是全局稳定的，当且仅当算子是幺模（阵）算子。

定义11表示如果系统P存在右分解P=ND-1，且N和D满足Bezout等式SN+RD=M,M为幺模算子，那么该系统是全局稳定的。

然而，在满足Bezout等式2-13后，可以得到图2-5的等效系统图。输出和参考输入关系可以表示成如下的式子[7]：

如果输出空间和参考输入空间相同，即：

图2-6　非线性反馈控制系统的等效系统图

那么系统的输出就能跟踪上输入信号。由于用此方法设计的控制器S和R，既满足互质分解，也能保证系统的输出信号跟踪性能，简单地称条件式（2-9）为一般条件[7]。