算子（演算子）理论是一种控制理论，它的基本思想是以映射为基础，将一个信号从输入空间映射至输出空间[1～6]。算子理论目前较为先进，与其相对应的控制对象不必再做近似线性化处理。通常来说，函数是数集到数集的映射，演算子也是一种映射关系，但是是基于空间到空间的，它是对函数这一概念的进一步推广和研究。非线性的演算子的定义由de Figueiredo等学者提出，这种定义使得我们在应用中无需再对非线性对象做线性化的处理，方便、适合运用到真实的工业环境之中[7～11]。

2.1.1　定义1：演算子

如图2-1所示，P为一个非线性演算子，Q为X→Y的映射。其中，X为演算子P的输入空间，Y为演算子P的输出空间。X、Y都是赋范的线性空间。从数学的角度描述，y（t）=Q（u）（t）。其中，u（t）为X中的元素，y（t）为Y中元素。

图2-1　演算子

2.1.2　定义2：输入输出有界稳定（BIBO：Bounded-input Bounded-output）

如图2-2所示，Q为一个稳定算子。令X、Y为实数域的线性空间，令XS、YS为标准线性子空间，分别称为X、Y的稳定子空间。一般的，定义XS=x∈X：{‖x‖＜∞}，YS={y∈Y：‖y‖＜∞}。一般地，若P（XS）⊆YS，则算子Q：X→Y称为BIBO[8]。

图2-2　稳定算子与输入输出有界稳定

赋范线性空间就是定义了范数的线性空间，所谓范数就是线性空间到数域的一个映射，其满足范数公理（正定性，齐次性，三角不等式）。

2.1.3　定义3：赋范线性空间

设E是实数域（或复数域）K上的线性空间。若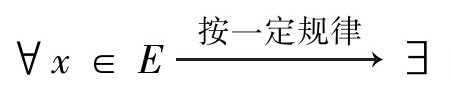实数‖x‖≥0，且满足以下范数公理[8]：

（1）正定性：‖x‖≥0，当且仅当x=0时，‖x‖=0；

（2）齐次性：‖αx‖=α·‖x‖；

（3）三角不等式：∀x,y∈E，有‖x+y‖≤‖x‖+‖y‖。

则把‖x‖当作是x的范数、E是赋范线性空间，表示为（E，‖x‖）或E。

2.1.4　定义4：算子P的范数

算子P的范数表示为[8]：

也可表示为式（2-2）：

2.1.5　定义5：单模算子

令S（X,Y）为X→Y上的稳定算子，则存在S（X,Y）的子集u（X,Y）：(www.daowen.com)

u（X,Y）={M：M∈S（X,Y）}

（2-3）

式中：M可逆且M-1∈S（Y,X）；u（X,Y）中的元素M称为单模算子[8]。

下面将对广义Lipschitz算子进行介绍，它是定义在扩展性空间的算子。

2.1.6　定义6：截断算子

令Z为包含定义在区间[0，+∞）上的所有实值可测函数的线性空间。对任意常数T∈[0，+∞），令PT为从线性空间Z映射到另一包含可测函数的线性空间ZT的投影算子：

式中：fT（t）∈ZT称为f（t）的截断。对于任意给定的可测函数的Banach空间X，设：

显然，Xe为Z的线性子空间，它是Banach空间X的扩展线性空间。

值得注意的是，扩展线性空间并不是Banach空间，但是它由相关的Banach空间决定。扩展线性空间之所以应用广泛，是因为在实际运用中，所有控制信号均是有限时间连续的。

2.1.7　定义7：广义的Lipschitz算子

令Xe、Ye为两个扩展的Banach空间，它们与定义在[0，+∞）上的实数域函数的Banach空间相关联，且有子空间U满足U⊆Ye。非线性算子P：U→Ye被称为U上的广义Lipschitz算子[8]。

如果存在常数c满足：

式中：∀x,s∈U且T∈[0，∞）。这样最小的c由下式决定：

c被称为广义Lipschitz算子的子范数和非线性算子P的实范数。

非线性算子的实范数由下式定义：

此外，如果一个Lipschitz算子是稳定的，那么它被称为是有限增益稳定的。由式（2-5）可以得到：

因标准Lipschize算子与广义Lipschize算子范围与域并不相同，所以二者并无可比性。对于非线性系统输入控制信号的稳定性、鲁棒性、唯一性的控制及设计方面而言，广义Lip-schize算子比标准Lipschize算子更具实用性。

我们声明，本书中所有的有界线性算子是广义Lipschitz算子。我们并不是只考虑有限增益稳定，因为输入空间中的输入函数可能被映射到它的变化范围内的某个地方，而不在其输出空间中，所以一个有限增益算子在上述定义7下可能是不稳定的[3]。